题目内容
【题目】已知函数![]() ,直线l:
,直线l:![]() .
.
![]() 求
求![]() 的单调增区间;
的单调增区间;
![]() 求证:对于任意
求证:对于任意![]() ,直线l都不是线
,直线l都不是线![]() 的切线;
的切线;
![]() 试确定曲线
试确定曲线![]() 与直线l的交点个数,并说明理由.
与直线l的交点个数,并说明理由.
【答案】(1)单调增区间为![]() ,
,![]() ;(2)见证明;(3)见解析
;(2)见证明;(3)见解析
【解析】
![]() 求出函数
求出函数![]() 定义域,求导,令
定义域,求导,令![]() ,即可求得函数的单调增区间;
,即可求得函数的单调增区间;
![]() 假设存在某个
假设存在某个![]() ,使得直线l与曲线
,使得直线l与曲线![]() 相切,设切点为
相切,设切点为![]() ,求出切线满足斜率,推出
,求出切线满足斜率,推出![]() ,此方程显然无解,假设不成立
,此方程显然无解,假设不成立![]() 推出直线l都不是曲线
推出直线l都不是曲线![]() 的切线;
的切线;
![]() “曲线
“曲线![]() 与直线l的交点个数”等价于“方程
与直线l的交点个数”等价于“方程![]() 的根的个数”,令
的根的个数”,令![]() ,则
,则![]() ,其中
,其中![]() ,且
,且![]() 函数
函数![]() ,其中
,其中![]() ,求出导数,判断函数的单调性,然后推出曲线
,求出导数,判断函数的单调性,然后推出曲线![]() 与直线l交点个数.
与直线l交点个数.
,![]() 解:函数
解:函数![]() 定义域为
定义域为![]() ,
,
![]() ,
,
由![]() ,解得
,解得![]() 或
或![]() .
.
![]() 函数
函数![]() 的单调增区间为
的单调增区间为![]() ,
,![]() ;
;
![]() 证明:假设存在某个
证明:假设存在某个![]() ,使得直线l与曲线
,使得直线l与曲线![]() 相切,
相切,
设切点为![]() ,
,
又![]() ,
,
![]() 切线满足斜率
切线满足斜率![]() ,且过点A,
,且过点A,
![]() ,
,
即![]() ,此方程显然无解,
,此方程显然无解,
![]() 假设不成立.
假设不成立.
故对于任意![]() ,直线l都不是曲线
,直线l都不是曲线![]() 的切线;
的切线;
![]() 解:“曲线
解:“曲线![]() 与直线l的交点个数”等价于“方程
与直线l的交点个数”等价于“方程![]() 的根的个数”.
的根的个数”.
由方程![]() ,得
,得![]() .
.
令![]() ,则
,则![]() ,其中
,其中![]() ,且
,且![]() .
.
考察函数![]() ,其中
,其中![]() ,
,
![]() ,
,
![]() 函数
函数![]() 在R单调递增,且
在R单调递增,且![]() .
.
而方程![]() 中,
中,![]() ,且
,且![]() .
.
![]() 当
当![]() 时,方程
时,方程![]() 无根;当
无根;当![]() 时,方程
时,方程![]() 有且仅有一根,
有且仅有一根,
故当![]() 时,曲线
时,曲线![]() 与直线l没有交点,
与直线l没有交点,
而当![]() 时,曲线
时,曲线![]() 与直线l有且仅有一个交点.
与直线l有且仅有一个交点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某地区某农产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
年产量y(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(Ⅰ)根据表中数据,建立![]() 关于的线性回归方程
关于的线性回归方程![]() ;
;
(Ⅱ)根据线性回归方程预测2019年该地区该农产品的年产量.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: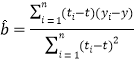 ,
,![]() .(参考数据:
.(参考数据:![]() ,计算结果保留小数点后两位)
,计算结果保留小数点后两位)

