题目内容
已知椭圆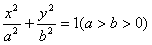 长轴长与短轴长之差是2
长轴长与短轴长之差是2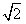 -2,且右焦点F到此椭圆一个短轴端点的距离为
-2,且右焦点F到此椭圆一个短轴端点的距离为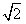 ,点C(m,0)是线段OF上的一个动点(O为坐标原点)。
,点C(m,0)是线段OF上的一个动点(O为坐标原点)。
(Ⅰ)求椭圆的方程;
(Ⅱ)是否存在过点F且与x轴不垂直的直线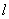 与椭圆交于A、B两点,使得
与椭圆交于A、B两点,使得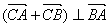 ,并说明理由。
,并说明理由。
【注:当直线BA的斜率存在且为k时,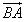 的方向向量可表示为(1,k)】
的方向向量可表示为(1,k)】
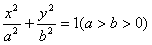 长轴长与短轴长之差是2
长轴长与短轴长之差是2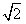 -2,且右焦点F到此椭圆一个短轴端点的距离为
-2,且右焦点F到此椭圆一个短轴端点的距离为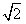 ,点C(m,0)是线段OF上的一个动点(O为坐标原点)。
,点C(m,0)是线段OF上的一个动点(O为坐标原点)。(Ⅰ)求椭圆的方程;
(Ⅱ)是否存在过点F且与x轴不垂直的直线
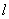 与椭圆交于A、B两点,使得
与椭圆交于A、B两点,使得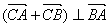 ,并说明理由。
,并说明理由。 【注:当直线BA的斜率存在且为k时,
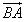 的方向向量可表示为(1,k)】
的方向向量可表示为(1,k)】 解:(Ⅰ)由题意可知 ,
,
又 ,解得:a=
,解得:a= ,b=c=1,
,b=c=1,
∴椭圆的方程为 。
。
(Ⅱ)由(Ⅰ)得F(1,0),所以0≤m≤1,
假设存在满足题意的直线l,设l的方程为y=k(x-1),
代入 ,得
,得 ,
,
设 ,则
,则 , ①
, ①
∴ ,
,
∴ ,
,

而AB的方向向量为(1,k),
∴ ,
,
∴当 时,
时, ,即存在这样的直线l;
,即存在这样的直线l;
当 时,k不存在,即不存在这样的直线l。
时,k不存在,即不存在这样的直线l。
 ,
,又
 ,解得:a=
,解得:a= ,b=c=1,
,b=c=1,∴椭圆的方程为
 。
。(Ⅱ)由(Ⅰ)得F(1,0),所以0≤m≤1,
假设存在满足题意的直线l,设l的方程为y=k(x-1),
代入
 ,得
,得 ,
,设
 ,则
,则 , ①
, ①∴
 ,
,∴
 ,
,
而AB的方向向量为(1,k),
∴
 ,
,∴当
 时,
时, ,即存在这样的直线l;
,即存在这样的直线l;当
 时,k不存在,即不存在这样的直线l。
时,k不存在,即不存在这样的直线l。
练习册系列答案
相关题目