题目内容
已知a>b>c,且a+b+c=0,求证: a.
a.
 a.
a.见解析
要证 a,只需证b2-ac<3a2.∵a+b+c=0,∴只需证b2+a(a+b)<3a2,只需证2a2-ab-b2>0,只需证(a-b)(2a+b)>0,只需证(a-b)(a-c)>0.∵a>b>c,∴a-b>0,a-c>0,∴(a-b)(a-c)>0显然成立.故原不等式成立.
a,只需证b2-ac<3a2.∵a+b+c=0,∴只需证b2+a(a+b)<3a2,只需证2a2-ab-b2>0,只需证(a-b)(2a+b)>0,只需证(a-b)(a-c)>0.∵a>b>c,∴a-b>0,a-c>0,∴(a-b)(a-c)>0显然成立.故原不等式成立.
 a,只需证b2-ac<3a2.∵a+b+c=0,∴只需证b2+a(a+b)<3a2,只需证2a2-ab-b2>0,只需证(a-b)(2a+b)>0,只需证(a-b)(a-c)>0.∵a>b>c,∴a-b>0,a-c>0,∴(a-b)(a-c)>0显然成立.故原不等式成立.
a,只需证b2-ac<3a2.∵a+b+c=0,∴只需证b2+a(a+b)<3a2,只需证2a2-ab-b2>0,只需证(a-b)(2a+b)>0,只需证(a-b)(a-c)>0.∵a>b>c,∴a-b>0,a-c>0,∴(a-b)(a-c)>0显然成立.故原不等式成立.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,b=2-x,c=x2-x+1,试证明a,b,c至少有一个不小于1.
,b=2-x,c=x2-x+1,试证明a,b,c至少有一个不小于1. 是一个自然数,
是一个自然数, 是
是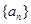 :
: 是自然数,
是自然数, (
( ,
, ).
). ,
, ;
; ,求证:
,求证: ;
; 时,求证:存在
时,求证:存在 ,使得
,使得 .
. an+n-4,λ∈R,n∈N+,对任意λ
an+n-4,λ∈R,n∈N+,对任意λ
 >
> ”时,假设的内容应为______________.
”时,假设的内容应为______________. ,且
,且 求证:
求证: 中至少有一个是负数。
中至少有一个是负数。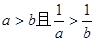 ,则
,则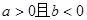 .
.