题目内容
已知点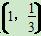 是函数f(x)=ax(a>0,且a≠1)的图像上一点,等比数列{an}的前n项和为f(n)-c,数列{bn}(bn>0)的首项为c,且前n项和Sn满足:Sn-Sn-1=
是函数f(x)=ax(a>0,且a≠1)的图像上一点,等比数列{an}的前n项和为f(n)-c,数列{bn}(bn>0)的首项为c,且前n项和Sn满足:Sn-Sn-1=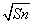 +
+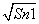 (n≥2).
(n≥2).
(1)求数列{an}和{bn}的通项公式;
(2)若数列{cn}的通项cn=bn· n,求数列{cn}的前n项和Rn.
n,求数列{cn}的前n项和Rn.
解:(1)∵f(1)=a=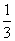 ,∴f(x)=
,∴f(x)= x,
x,
a1=f(1)-c=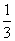 -c,
-c,
a2=[f(2)-c]-[f(1)-c]=-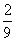 ,
,
a3=[f(3)-c]-[f(2)-c]=-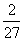 .
.
又数列{an}成等比数列,
∴a1=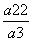 =
=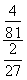 =-
=-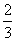 =
=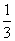 -c,∴c=1.
-c,∴c=1.
又公比q=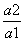 =
=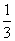 ,∴an=-
,∴an=-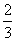
 n-1=-2
n-1=-2 n(n∈N*).
n(n∈N*).
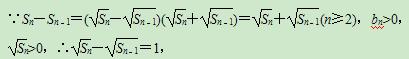 ∴数列{
∴数列{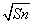 }构成一个首项为1,公差为1的等差数列,
}构成一个首项为1,公差为1的等差数列,
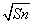 =1+(n-1)×1=n,Sn=n2.
=1+(n-1)×1=n,Sn=n2.
当n≥2时,bn=Sn-Sn-1=n2-(n-1)2=2n-1;
又b1=c=1满足bn=2n-1,
∴bn=2n-1(n∈N*).
(2)∵cn=bn n=(2n-1)
n=(2n-1) n,
n,
∴Rn=c1+c2+c3+…+cn,
Rn=1× 1+3×
1+3× 2+5×
2+5× 3+…+(2n-1)×
3+…+(2n-1)× n,①
n,①
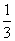 Rn=1×
Rn=1× 2+3×
2+3× 3+5×
3+5× 4+…+(2n-3)×
4+…+(2n-3)× n+(2n-1)×
n+(2n-1)× n+1.②
n+1.②
由①-②得,
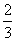 Rn=
Rn=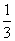 +2
+2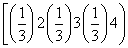
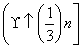 -(2n-1)×
-(2n-1)× n+1,
n+1,
化简得,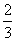 Rn=
Rn=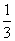 +2×
+2×


练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目

 B.-
B.- D.-
D.- -(2n-1)an-2n=0.
-(2n-1)an-2n=0. ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.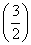 n-1
n-1 的离心率为
的离心率为 ,则其渐近线的斜率为( )
,则其渐近线的斜率为( ) B.
B. C.
C. D.
D.
 ,
, ,若
,若 ∥
∥ ,则
,则
 B.
B. C.
C. D.
D.
 B.
B.  C.
C.  D.
D. 
 <
< <0,则下列结论不正确的是( )
<0,则下列结论不正确的是( )