题目内容
已知函数f(x)=ax2+bx+
.若a∈(1,2,3),b∈(-4,-2,2,4),求f(x)的顶点落在第四象限的概率.
| 1 |
| 2 |
考点:古典概型及其概率计算公式
专题:概率与统计
分析:根据二次函数性质,利用列举法求解.
解答:
解:f(x)=ax2+bx+
顶点坐标为 (-
,
),
当a=1时,b=-4 点坐标为(2,-3)在第四象限,
a=1时,b=-2 点坐标为(1,-
)在第四象限,
a=1时,b=2点坐标为(-1,-
)在第三象限,
a=1时,b=4点坐标为(-2,-3)在第四象限,
a=2时,b=-4点坐标为(1,-
)在第四象限,
a=2时,b=-2点坐标为(
,0)在X轴上,
a=2时,b=-2点坐标为(-
,0)在x轴上,
a=2时,b=4点坐标为(-1,-
)在第三象限,
a=3时,b=-4点坐标为(
,
)在第一象限,
a=3时,b=-2点坐标为(
,
)在第一象限,
a=3时,b=2点坐标为(-
,
)在第二象限,
a=3时,b=-4点坐标为(-
,
)在第二象限.
故在项点在第四象限的概率为
.
| 1 |
| 2 |
| b |
| 2a |
| 2a-b2 |
| 4a |
当a=1时,b=-4 点坐标为(2,-3)在第四象限,
a=1时,b=-2 点坐标为(1,-
| 1 |
| 2 |
a=1时,b=2点坐标为(-1,-
| 1 |
| 2 |
a=1时,b=4点坐标为(-2,-3)在第四象限,
a=2时,b=-4点坐标为(1,-
| 3 |
| 2 |
a=2时,b=-2点坐标为(
| 1 |
| 2 |
a=2时,b=-2点坐标为(-
| 1 |
| 2 |
a=2时,b=4点坐标为(-1,-
| 3 |
| 2 |
a=3时,b=-4点坐标为(
| 2 |
| 3 |
| 1 |
| 6 |
a=3时,b=-2点坐标为(
| 1 |
| 3 |
| 1 |
| 6 |
a=3时,b=2点坐标为(-
| 1 |
| 3 |
| 1 |
| 6 |
a=3时,b=-4点坐标为(-
| 2 |
| 3 |
| 5 |
| 6 |
故在项点在第四象限的概率为
| 1 |
| 4 |
点评:本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
曲线y=x3+x2+x+1在点(-1,0)处的切线与抛物线y=ax2(a≠0)相切,则抛物线的准线方程是( )
A、y=-
| ||
B、y=
| ||
C、x=-
| ||
D、x=
|



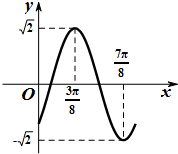 已知函数f(x)=asin(ωx+θ)的部分图象如下图,其中ω>0,|θ|<
已知函数f(x)=asin(ωx+θ)的部分图象如下图,其中ω>0,|θ|<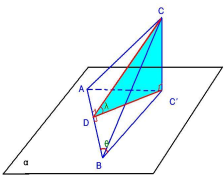 如图,已知△ABC在平面α内的射影为△ABC′,若∠ABC′=θ,BC′=a,且平面ABC与平面α所成的角为λ,求点C到平面α的距离.
如图,已知△ABC在平面α内的射影为△ABC′,若∠ABC′=θ,BC′=a,且平面ABC与平面α所成的角为λ,求点C到平面α的距离.