题目内容
四棱锥P-ABCD的底面ABCD是平行四边形, =(-1,2,1),
=(-1,2,1), =(0,-2,3),
=(0,-2,3), ═(8,3,2),
═(8,3,2),
(1)求证:PA⊥底面ABCD;
(2)求PC的长.
证明:(1)∵ =(-1,2,1),
=(-1,2,1), =(0,-2,3),
=(0,-2,3), ═(8,3,2),
═(8,3,2),
∴ ,
,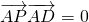 ,
,
∴ ,
,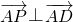 ,
,
即AP⊥AB且AP⊥AD,
又∵AB∩AD=A
∴AP⊥平面ABCD;
(2)∵ =(-1,2,1),
=(-1,2,1), =(0,-2,3),
=(0,-2,3), ═(8,3,2),
═(8,3,2),
∴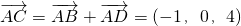 ,
,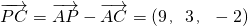 ,
,
∴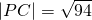 .
.
(1)由已知中向量 =(-1,2,1),
=(-1,2,1), =(0,-2,3),
=(0,-2,3), ═(8,3,2),根据两个向量的数量积为0,两个向量垂直,我们可以判断出AP⊥AB且AP⊥AD,进而根据线面垂直的判定定理得到PA⊥底面ABCD;
═(8,3,2),根据两个向量的数量积为0,两个向量垂直,我们可以判断出AP⊥AB且AP⊥AD,进而根据线面垂直的判定定理得到PA⊥底面ABCD;
(2)由已知中向量 =(-1,2,1),
=(-1,2,1), =(0,-2,3),
=(0,-2,3), ═(8,3,2),根据向量加法的三角形法则,可以求出向量PC的坐标,进而代入向量模的计算公式,得到答案.
═(8,3,2),根据向量加法的三角形法则,可以求出向量PC的坐标,进而代入向量模的计算公式,得到答案.
点评:本题考查的知识点是向量语言表述线线垂直的关系,空间点到点距离的运算,其中(1)中证得AP⊥AB且AP⊥AD是关键,(2)中计算出向量PC的坐标是关键.
 =(-1,2,1),
=(-1,2,1), =(0,-2,3),
=(0,-2,3), ═(8,3,2),
═(8,3,2),∴
 ,
,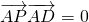 ,
,∴
 ,
,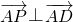 ,
,即AP⊥AB且AP⊥AD,
又∵AB∩AD=A
∴AP⊥平面ABCD;
(2)∵
 =(-1,2,1),
=(-1,2,1), =(0,-2,3),
=(0,-2,3), ═(8,3,2),
═(8,3,2),∴
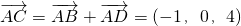 ,
,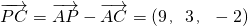 ,
,∴
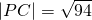 .
.(1)由已知中向量
 =(-1,2,1),
=(-1,2,1), =(0,-2,3),
=(0,-2,3), ═(8,3,2),根据两个向量的数量积为0,两个向量垂直,我们可以判断出AP⊥AB且AP⊥AD,进而根据线面垂直的判定定理得到PA⊥底面ABCD;
═(8,3,2),根据两个向量的数量积为0,两个向量垂直,我们可以判断出AP⊥AB且AP⊥AD,进而根据线面垂直的判定定理得到PA⊥底面ABCD;(2)由已知中向量
 =(-1,2,1),
=(-1,2,1), =(0,-2,3),
=(0,-2,3), ═(8,3,2),根据向量加法的三角形法则,可以求出向量PC的坐标,进而代入向量模的计算公式,得到答案.
═(8,3,2),根据向量加法的三角形法则,可以求出向量PC的坐标,进而代入向量模的计算公式,得到答案.点评:本题考查的知识点是向量语言表述线线垂直的关系,空间点到点距离的运算,其中(1)中证得AP⊥AB且AP⊥AD是关键,(2)中计算出向量PC的坐标是关键.

练习册系列答案
相关题目
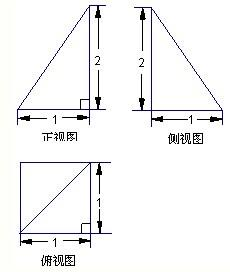 已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )
已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )A、
| ||
| B、1 | ||
C、
| ||
D、
|
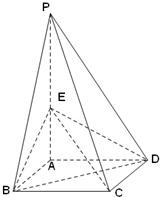 如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点. 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE=
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE= 如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证: