题目内容
设函数f(x)=(x _ 1)ex _ kx2(k∈R).
(Ⅰ)当k=1时,求函数f(x)的单调区间;
(Ⅱ)当k∈(1/2,1]时,求函数f(x)在[0,k]上的最大值M.
(Ⅰ)函数 的递减区间为
的递减区间为 ,递增区间为
,递增区间为 ,
, .
.
(Ⅱ)函数 在
在 上的最大值
上的最大值 .
.
解析试题分析:(Ⅰ) 当 时,
时,  ,
,
令 ,得
,得 ,
,
当 变化时,
变化时,  的变化如下表:
的变化如下表:
由表可知,函数













极大值 
极小值 
 的递减区间为
的递减区间为 ,递增区间为
,递增区间为 ,
, . 6分
. 6分
(Ⅱ)  ,
,
令 ,得
,得 ,
, ,
,
令 ,则
,则 ,所以
,所以 在
在 上递增,
上递增,
所以 ,从而
,从而 ,所以
,所以
所以当 时,
时,  ;当
;当

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
 为函数
为函数 图象上一点,O为坐标原点,记直线
图象上一点,O为坐标原点,记直线 的斜率
的斜率 .
. 在区间
在区间
 上存在极值,求实数m的取值范围;
上存在极值,求实数m的取值范围; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; .
. .
. 时,
时, ,求
,求 的最小值;
的最小值; 的通项
的通项 ,证明:
,证明: .
.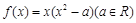 ,
,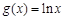 .
.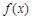 在
在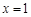 处取得极值,求
处取得极值,求 上
上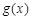 图像的上方(没有公共点),求实数
图像的上方(没有公共点),求实数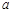 的取值范围.
的取值范围.  .
.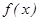 的单调区间;
的单调区间; 的图象在点(2,f(2))处的切线的倾斜角为45o,对于任意的t
的图象在点(2,f(2))处的切线的倾斜角为45o,对于任意的t [1,2],函数
[1,2],函数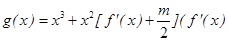 是
是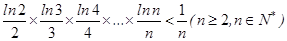
 与
与 在
在 处的切线互相垂直,求
处的切线互相垂直,求 的值.
的值.
 的单调递减区间为
的单调递减区间为 ,求函数
,求函数 ,
,
 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围 在
在 与
与 时都取得极值
时都取得极值 函数f(x)的极值;
函数f(x)的极值; ,方程
,方程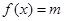 恰好有三个根,求
恰好有三个根,求 的取值范围.
的取值范围.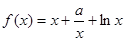 ,
, 时,求函数
时,求函数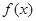 的单调增区间;
的单调增区间;