题目内容
已知向量
，令f（x）=
．
（1）当
时，求f（x）的值域；
（2）已知
，求
的值．
解（1）∵f（x）==cos2x
=
=cos2x+
sin2x
∴
，
∵，
∴
∴
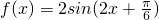∴y=f（x）的值域为（-1，2]； …（7分）
（2）由
∴
（14分）．
分析：（1）由f（x）==cos2x，利用二倍角公式、辅助角公式对三角函数进行化简，然后结合，及正弦函数的性质可求函数的值域
（2）由已知可得sin（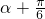
）=
，然后由cos（2α
）=cos[2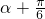（）-π]，利用诱导公式及二倍角公式可求
点评：本题主要考查了向量的数量积的坐标表示，正弦函数的性质的应用，二倍角公式、辅助角公式的综合应用．
=cos2x=
=cos2x+
sin2x∴
，∵
，∴
∴
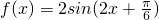∴y=f（x）的值域为（-1，2]； …（7分）
（2）由
∴
（14分）．分析：（1）由f（x）=
=cos2x，利用二倍角公式、辅助角公式对三角函数进行化简，然后结合，及正弦函数的性质可求函数的值域（2）由已知可得sin（
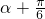）=，然后由cos（2α）=cos[2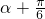（）-π]，利用诱导公式及二倍角公式可求点评：本题主要考查了向量的数量积的坐标表示，正弦函数的性质的应用，二倍角公式、辅助角公式的综合应用．
练习册系列答案
相关题目
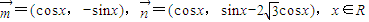，令f（x）=
，
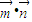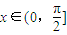时，求函数f（x）的值域．
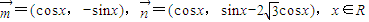，令f（x）=
，
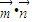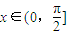时，求函数f（x）的值域．
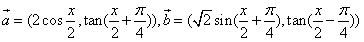，令f（x）=
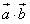，是否存在实数x∈[0，π]，使f（x）+f′（x）=0（其中f′（x）是f（x）的导函数）？若存在，则求出x的值；若不存在，则证明之。
，令f（x）=
，求函数f(x)的最大值，最小正周期，并写出f(x)在[0，π]上的单调区间。