题目内容
已知向量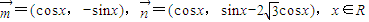 ,令f(x)=
,令f(x)=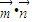 ,
,(Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)当
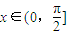 时,求函数f(x)的值域.
时,求函数f(x)的值域.
【答案】分析:(Ⅰ)先根据 表示出函数的解析式,进而利用两角和公式和二倍角公式化简整理,进而根据正弦函数的单调性求得函数的单调递增区间.
表示出函数的解析式,进而利用两角和公式和二倍角公式化简整理,进而根据正弦函数的单调性求得函数的单调递增区间.
(Ⅱ)根据x的范围确定2x+ 的范围,进而利用正弦定理的单调性求得函数的最大值和最小值,进而求得函数的值域.
的范围,进而利用正弦定理的单调性求得函数的最大值和最小值,进而求得函数的值域.
解答:解:(Ⅰ)f(x)= =
= =
=
∵函数y=sinx的单调增区间为 ,
,
∴ ,∴
,∴ ,k∈Z
,k∈Z
∴函数f(x)的单调递增区间为 ,k∈Z
,k∈Z
(Ⅱ)当 时,
时,
∴ ,
,
∴ ,
,
即
∴函数f(x)的值域为[-1,2]
点评:本题主要考查了正弦函数的单调性,和两角和公式,二倍角公式等的运用.三角函数的基本公式较多,平时应注意多积累.
 表示出函数的解析式,进而利用两角和公式和二倍角公式化简整理,进而根据正弦函数的单调性求得函数的单调递增区间.
表示出函数的解析式,进而利用两角和公式和二倍角公式化简整理,进而根据正弦函数的单调性求得函数的单调递增区间.(Ⅱ)根据x的范围确定2x+
 的范围,进而利用正弦定理的单调性求得函数的最大值和最小值,进而求得函数的值域.
的范围,进而利用正弦定理的单调性求得函数的最大值和最小值,进而求得函数的值域.解答:解:(Ⅰ)f(x)=
 =
= =
=
∵函数y=sinx的单调增区间为
 ,
,∴
 ,∴
,∴ ,k∈Z
,k∈Z∴函数f(x)的单调递增区间为
 ,k∈Z
,k∈Z(Ⅱ)当
 时,
时,∴
 ,
,∴
 ,
,即

∴函数f(x)的值域为[-1,2]
点评:本题主要考查了正弦函数的单调性,和两角和公式,二倍角公式等的运用.三角函数的基本公式较多,平时应注意多积累.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
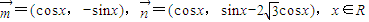 ,令f(x)=
,令f(x)=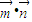 ,
,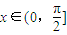 时,求函数f(x)的值域.
时,求函数f(x)的值域. ,令f(x)=
,令f(x)= .
. 时,求f(x)的值域;
时,求f(x)的值域; ,求
,求 的值.
的值.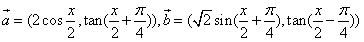 ,令f(x)=
,令f(x)=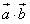 ,是否存在实数x∈[0,π],使f(x)+f′(x)=0(其中f′(x)是f(x)的导函数)?若存在,则求出x的值;若不存在,则证明之。
,是否存在实数x∈[0,π],使f(x)+f′(x)=0(其中f′(x)是f(x)的导函数)?若存在,则求出x的值;若不存在,则证明之。 ,令f(x)=
,令f(x)= ,求函数f(x)的最大值,最小正周期,并写出f(x)在[0,π]上的单调区间。
,求函数f(x)的最大值,最小正周期,并写出f(x)在[0,π]上的单调区间。