题目内容
已知向量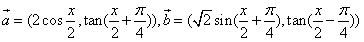
，令f（x）=
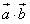，是否存在实数x∈[0，π]，使f（x）+f′（x）=0（其中f′（x）是f（x）的导函数）？若存在，则求出x的值；若不存在，则证明之。
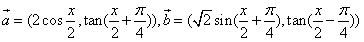，令f（x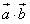）=，是否存在实数x∈[0，π]，使f（x）+f′（x）=0（其中f′（x）是f（x）的导函数）？若存在，则求出x的值；若不存在，则证明之。解：
，
令f（x）+f′（x）=0，
即f（x）+f′（x）=sinx+cosx+cosx-sinx=2cosx=0，
可得
，
所以存在实数
∈[0，π]，使f（x）+f′（x）=0。
，令f（x）+f′（x）=0，
即f（x）+f′（x）=sinx+cosx+cosx-sinx=2cosx=0，
可得
，所以存在实数
∈[0，π]，使f（x）+f′（x）=0。
练习册系列答案
阅读快车系列答案
相关题目
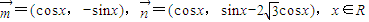，令f（x）=
，
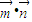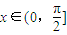时，求函数f（x）的值域．
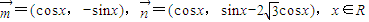，令f（x）=
，
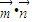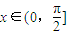时，求函数f（x）的值域．
，令f（x）=
．
时，求f（x）的值域；
，求
的值．
，令f（x）=
，求函数f(x)的最大值，最小正周期，并写出f(x)在[0，π]上的单调区间。