题目内容
直线x-2y+2=0与椭圆x2+4y2=4相交于A，B两点，则|AB|=________．
分析：直接利用直线与椭圆方程联立方程组，求出A，B的坐标，利用两点间距离公式求出距离即可．
解答：因为直线x-2y+2=0与椭圆x2+4y2=4相交于A，B两点，
所以
解得
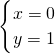或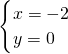
，A、B的坐标为（0，1），（-2，0），所以|AB|=
=故答案为：
；点评：本题考查直线与椭圆的交点坐标的求法，两点间距离公式的应用，也可以利用弦长公式求解．
练习册系列答案
相关题目
曲线
（θ为参数）上各点到直线x+2y-
=0的最大距离是（ ）
|
| 2 |
A、
| ||||
B、2
| ||||
C、3
| ||||
D、
|
两直线x-2y-2=0与x+y-1=0夹角的正切值是（ ）
A、-
| ||
| B、-3 | ||
C、
| ||
| D、3 |