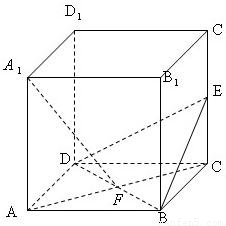
题目内容
已知:如图,在正方体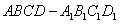 中,E是
中,E是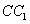 的中点,F是AC,BD 的交点。
的中点,F是AC,BD 的交点。
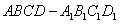 中,E是
中,E是 的中点,F是AC,BD 的交点。
的中点,F是AC,BD 的交点。 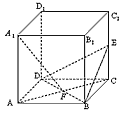
(1)求证:A1F⊥平面BED;
(2)求A1F与B1E所成角的余弦值。
(2)求A1F与B1E所成角的余弦值。
| (1)证明:由AA1⊥平面ABCD知,AF是A1F在平面ABCD上的射影, 又∵AC⊥BD, ∴A1F⊥BD, 取BC中点G,连结FG,B1G, ∵A1B1⊥平面BCC1B1,FG⊥平面BCC1B1, ∴B,G为A1F在面BCC1B1上的射影, 又正方形BCC1B1中,E,G分别为CC1,BC的中点, ∴BE⊥B1C, ∴  , ,又  , ,∴A1F⊥平面BED。 (2)解:  。 。 |
 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
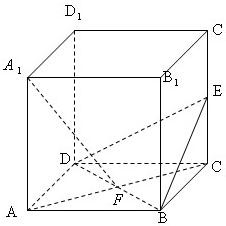 19、已知:如图,在正方体ABCD-A1B1C1D1中,E是CC1的中点,F是AC,BD的交点.
19、已知:如图,在正方体ABCD-A1B1C1D1中,E是CC1的中点,F是AC,BD的交点. 已知:如图,在单位正方体ABCD-A1B1C1D1中,M是A1B上的点,
已知:如图,在单位正方体ABCD-A1B1C1D1中,M是A1B上的点,