题目内容
设x,y,z是实数,3x,4y,5z成等比数列,且
,
,
成等差数列,则
+
的值是
.
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
| x |
| z |
| z |
| x |
| 34 |
| 15 |
| 34 |
| 15 |
分析:由题意可得到x与z之间的关系
=
,将等式左端展开整理即可得答案.
| (x+z)2 |
| xz |
| 64 |
| 15 |
解答:解:∵3x,4y,5z成等比数列,
∴16y2=15xz;
又
,
,
成等差数列,
∴y=
,
∴16×4x2z2=15xz(x+z)2,由xz≠0,得
=
,
∴
+
=
.
故答案为:
.
∴16y2=15xz;
又
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
∴y=
| 2xz |
| x+z |
∴16×4x2z2=15xz(x+z)2,由xz≠0,得
| (x+z)2 |
| xz |
| 64 |
| 15 |
∴
| x |
| z |
| z |
| x |
| 34 |
| 15 |
故答案为:
| 34 |
| 15 |
点评:本题考查等差数列与等比数列的概念,考查分析与转化运算的能力,属于中档题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 ,
, ,
, 成等差数列,则
成等差数列,则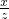 +
+ 的值是________.
的值是________. ,
, ,
, 成等差数列,则
成等差数列,则 +
+ 的值是 .
的值是 .