题目内容
已知等差数列 中,
中, ,
, ,数列
,数列 中,
中, ,
, .
.
(Ⅰ)求数列 的通项公式,写出它的前
的通项公式,写出它的前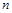 项和
项和 ;
;
(Ⅱ)求数列 的通项公式。
的通项公式。
 中,
中, ,
, ,数列
,数列 中,
中, ,
, .
.(Ⅰ)求数列
 的通项公式,写出它的前
的通项公式,写出它的前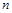 项和
项和 ;
;(Ⅱ)求数列
 的通项公式。
的通项公式。(1) ,
, ;
;
(2)
 ,
, ;
;(2)

试题分析:解:(I)设
 ,由题意得
,由题意得 ,
, ,
,所以
 ,
, ; 6分
; 6分(II)
 ,
, ,
,所以
 ,
, ,
,  (
( )
)又
 时
时 ,
,所以数列
 的通项
的通项 ; 12分
; 12分点评:主要是考查了等差数列的通项公式和求和的运用,属于基础题。

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 为等差数列,
为等差数列, +
+ +
+
 ,
,
 ,以
,以 表示
表示 项和,则使得
项和,则使得 }的前n项和为Sn,且
}的前n项和为Sn,且 的最小值为 .
的最小值为 . 中,若
中,若 是方程
是方程 的两个根,那么
的两个根,那么 的值为( )
的值为( )  是首项
是首项 的等比数列,且
的等比数列,且 ,
, ,
, 成等差数列.
成等差数列. ,设
,设 为数列
为数列 的前
的前 项和,若
项和,若 对一切
对一切 恒
恒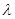 的最小值.
的最小值. 的第二项为8,前10项和为185。
的第二项为8,前10项和为185。 项,……按原来顺序组成一个新
项,……按原来顺序组成一个新 数列,试求数列
数列,试求数列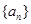 的前
的前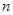 项和
项和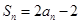 .数列
.数列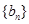 满足:
满足: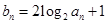 .
.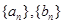 的通项
的通项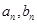 .并比较
.并比较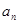 与
与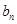 的大小;
的大小;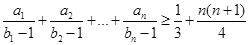 .
. 中,已知前15项的和
中,已知前15项的和 ,则
,则 等于_____________
等于_____________ 的
的 ,且
,且 ,则此数列
,则此数列


