题目内容
18.设集合A={(x,y)|ax+y=1},B={(x,y)|x+ay=1},C={(x,y)|x2+y2=1}.(1)当a为何值时,A∩C≠∅;
(2)当a为何值时,(A∪B)∩C是仅含有两个元素的集合;
(3)当a为何值时,(A∪B)∩C是仅含有三个元素的集合.
分析 (1)根据点到直线的距离即可判断,
(2)作出集合A,B的图象,利用(A∪B)∩C为两个元素的集合,说明①直线ax+y=1和x+ay=1与圆x2+y2=1各有一个交点且不重合,②直线ax+y=1和x+ay=1重合,且与圆x2+y2=1有两个不同的交点,求实数a即可;
(3)(A∪B)∩C为含三个元素的集合,a≠0,a≠1.直线ax+y=1和x+ay=1与圆x2+y2=1必须交于三个点,即两直线有一个交点在圆x2+y2=1上,且两直线与圆还各有一个交点,利用对称性求出实数a即可.
解答 解:∵集合A={(x,y)|ax+y=1},B={(x,y)|x+ay=1},C={(x,y)|x2+y2=1},
∴集合A,B表示直线,C表示单位圆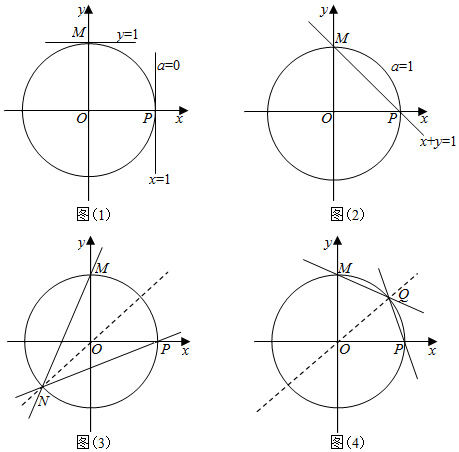
(1)∵A∩C≠∅,
∴直线与圆有交点,
∴d=$\frac{1}{\sqrt{{a}^{2}+1}}$≤1,
解得a为R,
(2)(A∪B)∩C含两个元素
①直线ax+y=1和x+ay=1与圆x2+y2=1各有一个交点且不重合,则满足条件,此时a=0,如图(1)所示
②直线ax+y=1和x+ay=1重合,且与圆x2+y2=1有两个不同的交点,则满足条件,此时a=1,如图(2)所示
综上,a=0或a=1时,(A∪B)∩C为含两个元素的集合
(2)(A∪B)∩C含三个元素
显然a≠0,a≠1.
直线ax+y=1和x+ay=1与圆x2+y2=1必须交于三个点,即两直线有一个交点在圆x2+y2=1上,且两直线与圆还各有一个交点
∵直线ax+y=1和x+ay=1关于直线y=x对称
∴三个交点为(0,1),(1,0),($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$)或(0,1),(1,0),(-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$)
如图(3)(4)所示
此时a=-1±$\sqrt{2}$
点评 本题考查子集、并集、交集的转换,考查数形结合,分类讨论的思想,转化思想的应用,作出图形,是解好本题的前提,是中档题.

 字词句段篇系列答案
字词句段篇系列答案| A. | 0 | B. | -1 | C. | 1 | D. | $\frac{1}{2}$ |
| A. | -$\frac{21}{20}$ | B. | -2 | C. | -$\frac{21}{10}$ | D. | -$\frac{21}{5}$ |