题目内容
(本小题满分14分)
已知直线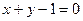 与椭圆
与椭圆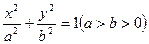 相交于
相交于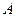 、
、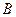 两点,
两点,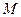 是线段
是线段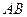 上的一点,
上的一点,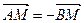 ,且点
,且点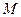 在直线
在直线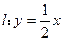 上.
上.
(1)求椭圆的离心率;
(2)若椭圆的焦点关于直线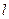 的对称点在单位圆
的对称点在单位圆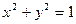 上,求椭圆的方程.
上,求椭圆的方程.
已知直线
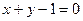 与椭圆
与椭圆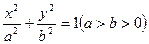 相交于
相交于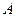 、
、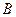 两点,
两点,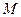 是线段
是线段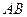 上的一点,
上的一点,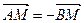 ,且点
,且点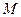 在直线
在直线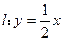 上.
上.(1)求椭圆的离心率;
(2)若椭圆的焦点关于直线
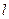 的对称点在单位圆
的对称点在单位圆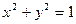 上,求椭圆的方程.
上,求椭圆的方程.(1)

(2)

解:
(1)有AN=-BN知M是AB的中点,
设A、B两点的坐标哦分别为 、
、 ,
,
由 { 得
得
根据根与系数的关系,的
则 .∴ 点
.∴ 点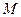 的坐标为
的坐标为 .…4分
.…4分
又∵ 点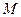 在直线
在直线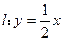 上,∴
上,∴  ,
,
∴
∴ ∴ 椭圆的离
∴ 椭圆的离 心率
心率 …………………7分
…………………7分
(2)由(1)知 ,由图形的对称性可知只需考虑一个焦点即可.
,由图形的对称性可知只需考虑一个焦点即可.
不妨设椭圆的一个焦点为 设
设 关于直线
关于直线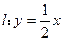 的对称点为
的对称点为 ,
,
则有 ,解得
,解得 …10
…10 分
分
由已知得 ∴ 有
∴ 有 , ∴
, ∴  .……12分
.……12分
又 ∴
∴ ∴ 所求的椭圆方程为
∴ 所求的椭圆方程为 . ……………14分
. ……………14分
(1)有AN=-BN知M是AB的中点,
设A、B两点的坐标哦分别为
 、
、 ,
,由 {
 得
得
根据根与系数的关系,的

则
 .∴ 点
.∴ 点 的坐标为
的坐标为 .…4分
.…4分又∵ 点
 在直线
在直线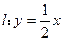 上,∴
上,∴  ,
, ∴

∴
 ∴ 椭圆的离
∴ 椭圆的离 心率
心率 …………………7分
…………………7分(2)由(1)知
 ,由图形的对称性可知只需考虑一个焦点即可.
,由图形的对称性可知只需考虑一个焦点即可.不妨设椭圆的一个焦点为
 设
设 关于直线
关于直线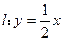 的对称点为
的对称点为 ,
,则有
 ,解得
,解得 …10
…10 分
分由已知得
 ∴ 有
∴ 有 , ∴
, ∴  .……12分
.……12分又
 ∴
∴ ∴ 所求的椭圆方程为
∴ 所求的椭圆方程为 . ……………14分
. ……………14分
练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
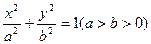 的离心率为
的离心率为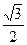 ,且过点(2,0)
,且过点(2,0)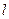 :
: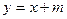 与椭圆C交于A、B两点,O为坐标原点,若
与椭圆C交于A、B两点,O为坐标原点,若 OAB为直角三角形,求
OAB为直角三角形,求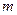 的值。
的值。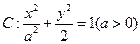 的左右焦点分别为
的左右焦点分别为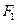 、
、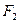 ,
,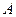 是椭圆
是椭圆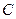 上的一点,
上的一点,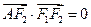 ,坐标原点
,坐标原点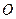 到直线
到直线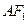 的距离为
的距离为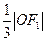 .
.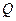 是椭圆
是椭圆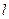 交
交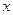 轴于点
轴于点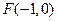 ,交
,交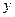 轴于点
轴于点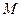 ,若
,若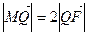 ,求直线
,求直线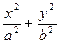 =1(
=1(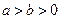 )上一点,
)上一点,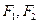 是椭圆的两焦点,且满足
是椭圆的两焦点,且满足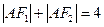 .
.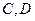 是椭圆上两点,直线
是椭圆上两点,直线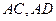 的倾斜角互补,求直线
的倾斜角互补,求直线 的斜率.
的斜率.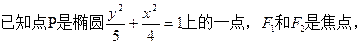
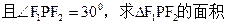 .
. (-3,0),
(-3,0),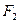 (3,0),点M满足
(3,0),点M满足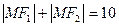 ,则M的轨迹方程为 ▲
,则M的轨迹方程为 ▲ 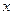 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为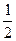 ,则
,则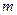 ="( " )
="( " ) .
. B.
B.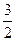 C.
C.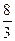 D.
D.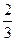
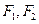 为椭圆
为椭圆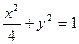 的两个焦点,点
的两个焦点,点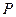 在椭圆上,且满足
在椭圆上,且满足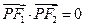 ,则
,则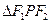 的面积是 ( )
的面积是 ( )