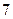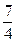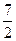题目内容
(本小题满分13分)
椭圆C: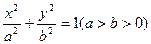 的离心率为
的离心率为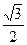 ,且过点(2,0)
,且过点(2,0)
(1)求椭圆C的方程;
(2)设直线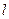 :
: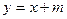 与椭圆C交于A、B两点,O为坐标原点,若
与椭圆C交于A、B两点,O为坐标原点,若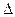 OAB为直角三角形,求
OAB为直角三角形,求 的值。
的值。
椭圆C:
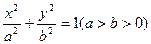 的离心率为
的离心率为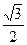 ,且过点(2,0)
,且过点(2,0)(1)求椭圆C的方程;
(2)设直线
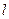 :
: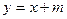 与椭圆C交于A、B两点,O为坐标原点,若
与椭圆C交于A、B两点,O为坐标原点,若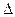 OAB为直角三角形,求
OAB为直角三角形,求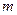 的值。
的值。(1)

(2)

解(1)依题意,可知 ,又
,又 ,所以可知
,所以可知
∴
故所求的椭圆方程为 ……………………………………………3分
……………………………………………3分
(2)联立方程 消去
消去 得
得 …………4分
…………4分
则 解得
解得
设 则
则 ,
,  ………………5分
………………5分
① 若 ,则可知
,则可知 ,即
,即
∴ 可解得
可解得
经检验 满足条件
满足条件
所以直线 满足题意…………………………………………………………9分
满足题意…………………………………………………………9分
② 若 ,则
,则 (或
(或 )
)
联立方程 解得
解得 或
或 ………………………10分
………………………10分
Ⅰ、若A( ,-
,- ) ,则可知
) ,则可知 -
-
Ⅱ、若B(- ,
,  ) ,则可知
) ,则可知

所以 也满足题意……………………………………………………………12分
也满足题意……………………………………………………………12分
综上可知 , 及
及 为所求的直线……………………………13分
为所求的直线……………………………13分
另解:② 若 ,则
,则 (或
(或 )
)
联立方程 解得
解得 ,………………………………………………10分
,………………………………………………10分
则点( 在
在 上,代入解得
上,代入解得 ,所以
,所以 也满足题意
也满足题意
 ,又
,又 ,所以可知
,所以可知
∴

故所求的椭圆方程为
 ……………………………………………3分
……………………………………………3分(2)联立方程
 消去
消去 得
得 …………4分
…………4分则
 解得
解得
设
 则
则 ,
,  ………………5分
………………5分① 若
 ,则可知
,则可知 ,即
,即
∴
 可解得
可解得
经检验
 满足条件
满足条件所以直线
 满足题意…………………………………………………………9分
满足题意…………………………………………………………9分② 若
 ,则
,则 (或
(或 )
)联立方程
 解得
解得 或
或 ………………………10分
………………………10分Ⅰ、若A(
 ,-
,- ) ,则可知
) ,则可知 -
-
Ⅱ、若B(-
 ,
,  ) ,则可知
) ,则可知

所以
 也满足题意……………………………………………………………12分
也满足题意……………………………………………………………12分综上可知 ,
 及
及 为所求的直线……………………………13分
为所求的直线……………………………13分另解:② 若
 ,则
,则 (或
(或 )
)联立方程
 解得
解得 ,………………………………………………10分
,………………………………………………10分则点(
 在
在 上,代入解得
上,代入解得 ,所以
,所以 也满足题意
也满足题意
练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
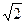 ),且过点
),且过点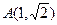 ,过A作倾斜角互补的两条直线,它们与椭圆的另一个交点分别为点B和点C。
,过A作倾斜角互补的两条直线,它们与椭圆的另一个交点分别为点B和点C。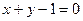 与椭圆
与椭圆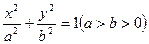 相交于
相交于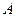 、
、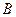 两点,
两点,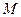 是线段
是线段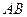 上的一点,
上的一点,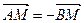 ,且点
,且点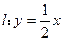 上.
上.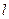 的对称点在单位圆
的对称点在单位圆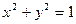 上,求椭圆的方程.
上,求椭圆的方程.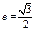 且椭圆经过
且椭圆经过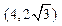 .
.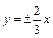 ,经过点
,经过点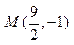 .
.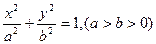 的左焦点,A(-a,0), B(0,b), 椭圆的离心率为
的左焦点,A(-a,0), B(0,b), 椭圆的离心率为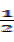 , 点D在x轴上,
, 点D在x轴上,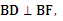 B,D,F三点确定的圆M恰好与直线l1:x+
B,D,F三点确定的圆M恰好与直线l1:x+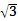 y+30相切
y+30相切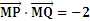 ,求直线l2的方程
,求直线l2的方程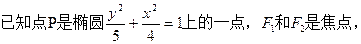
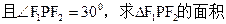 .
.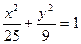 ,直线
,直线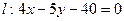 .椭圆上是否存在一点,它到直线
.椭圆上是否存在一点,它到直线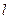 的距离最小?最小距离是多少?
的距离最小?最小距离是多少?



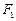 、
、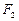 是椭圆
是椭圆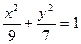 的两个焦点,
的两个焦点,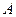 为椭圆上一点,且∠
为椭圆上一点,且∠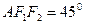 ,则Δ
,则Δ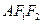 的面积为( )
的面积为( )