题目内容

已知x∈R,求证：ex≥x+1.

思路分析：构造函数f(x)=ex-x-1,只需证明f(x)≥0恒成立，利用函数的单调性求出函数的最小值就可以把问题解决了.

证明：令f(x)=ex-x-1,∴f′(x)=ex-1.

∵x∈［0,+∞),∴ex-1≥0恒成立,即f′(x)≥0.

∴f(x)为增函数.当x∈(-∞,0)时,f′(x)=ex-1＜0,

∴f(x)是减函数.又∵f(0)=0,

∴当x∈R时f(x)≥f(0),

即ex-x-1≥0,∴ex≥x+1.

练习册系列答案
相关题目
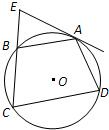精英家教网附加题：
A．如图，四边形ABCD内接于圆O，弧AB=弧AD，过A点的切线交CB的延长线于E点．
求证：AB2=BE•CD．
B．设数列{an}，{bn}满足an+1=3an+2bn，bn+1=2bn，且满足
an+4
bn+4
=M
an
bn
，试求二阶矩阵M．
C．已知椭圆C的极坐标方程为ρ2=
12
3cos2θ+4sin2θ
，点F1，F2为其左、右焦点，直线l的参数方程为
x=2+
2
2
t
y=
2
2
t
（t为参数，t∈R）．求点F1，F2到直线l的距离之和．
D．已知x，y，z均为正数．求证：
x
yz
+
y
zx
+
z
xy
≥
1
x
+
1
y
+
1
z
．
【选做题】在A，B，C，D四小题中只能选做2题，每小题10分，共计20分．请在答题卡指定区域内作答．解答应写出文字说明、证明过程或演算步骤．
A．选修4-1　几何证明选讲
如图，⊙O的直径AB的延长线与弦CD的延长线相交于点P，E为⊙O上一点，AE=AC，DE交AB于点F．求证：△PDF∽△POC．
B．选修4-2　矩阵与变换
若点A（2，2）在矩阵M=
cosα-sinα
sinαcosα
对应变换的作用下得到的点为B（-2，2），求矩阵M的逆矩阵．
C．选修4-4　坐标系与参数方程
已知极坐标系的极点O与直角坐标系的原点重合，极轴与x轴的正半轴重合，
曲线C1：ρcos(θ+
π
4
)=2
2
与曲线C2：
x=4t2
y=4t
（t∈R）交于A、B两点．求证：OA⊥OB．
D．选修4-5　不等式选讲
已知x，y，z均为正数．求证：
x
yz
+
y
zx
+
z
xy
≥
1
x
+
1
y
+
1
z
．
已知a∈R，函数f(x)=
a
x
+lnx-1，g（x）=（lnx-1）ex+x．
（1）求函数f（x）在区间（0，e]上的最小值；
（2）是否存在实数x0∈（0，e]，使曲线y=g（x）在点x=x0处的切线与y轴垂直？若存在，求出x0的值，若不存在，请说明理由；
（3）求证：(1+
1
2
+
1
3
+…+
1
n
)•
n
k=1
ln[k(k+1)(k+2)]＞(n-
1
4
)•ln
en
n!
      (n∈N*)．
已知a∈R，函数f（x）=ax-lnx，g(x)=
lnx
x
，x∈（0，e]，（其中e是自然对数的底数，为常数），
（1）当a=1时，求f（x）的单调区间与极值；
（2）在（1）的条件下，求证：f(x)＞g(x)+
1
2
；
（3）是否存在实数a，使得f（x）的最小值为3．若存在，求出a的值，若不存在，说明理由．
已知函数f（x）=（x-1）e-x，x∈R，其中e是自然对数的底数．
（Ⅰ）求函数f（x）的单调区间和极值；
（Ⅱ）若函数y=g（x）对任意x满足g（x）=f（4-x），求证：当x＞2时，f（x）＞g（x）；
（Ⅲ）若x1≠x2，且f（x1）=f（x2），求证：x1+x2＞4．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网