题目内容
一学生参加市场营销调查活动,从某商场得到11月份新款家电M的部分销售资料.资 料显示:11月2日开始,每天的销售量比前一天多t台(t为常数),期间某天由于商 家提高了家电M的价格,从当天起,每天的销售量比前一天少2台.11月份前2天 共售出8台,11月5日的销售量为18台.
(I)若商家在11月1日至15日之间未提价,试求这15天家电M的总销售量.
(II)若11月1日至15日的总销售量为414台,试求11月份的哪一天,该商场售出家电M的台数最多?并求这一天售出的台数.
解:(I)根据题意,商家在11月1日至15日之间家电M每天的销售量组成公差为t的等差数列{an},
∵ ,∴
,∴ ,解之得
,解之得
因此,这15天家电M的总销售量为S15=15×2+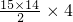 =450台.…(6分)
=450台.…(6分)
(II)设从11月1日起,第n天的销售量最多,1≤n≤30,n∈N*
由(I),若商家在11月1日至15日之间未提价,则这15天家电M的总销售量为450台,
而450>414不符合题意,故n<15;
若n=5,则S15=5×2+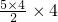 +10×16+
+10×16+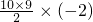 =120<414,
=120<414,
也不符合题意,故n>5
因此,前n天每天的销售量组成一个首项为2,公差为4的等差数列,第n+1天开始每天的销售量组成首项为4n-4,
公差为-2的等差数列.…(10分)
∴S15=[2n+ ]+[(15-n)(4n-4)+
]+[(15-n)(4n-4)+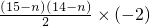 ]=-3n2+93n-270
]=-3n2+93n-270
由已知条件,得S15=414,即-3n2+93n-270=414
解之得n=15或n=19(舍去19)
∴n=12,出售家电M的台数为2+11×4=46台
故在11月12日,该商场售出家电M的台数最多,这一天的销售量为46台.
分析:(I)由题意,在11月1日至15日之间该商场家电M每天的销售量组成公差为t的等差数列{an},结合等差数列的通项公式解出首项a1和公差t,从而由等差数列求和公式得到这15天家电M的总销售量.
(II)设从11月1日起,第n天的销售量最多(1≤n≤30,n∈N*).根据(I)前15天的销售量大于414,可得n<15;通过假设n=5算出销售量为120<414,得n>5.因此n为大于5而小于15的整数,因此结合题中数据列出S15关于n的式子,解方程S15=414,即可得到n=15,可得在11月12日,该商场售出家电M的台数最多,这一天的销售量为46台.
点评:本题给出商场家电的销售量成等差数列的模型,求家电M哪一天的销售量为最多.着重考查了函数、数列的基本知识及其应用能力,考查了函数方程思想和转化化归思想的应用,属于中档题.
∵
 ,∴
,∴ ,解之得
,解之得
因此,这15天家电M的总销售量为S15=15×2+
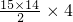 =450台.…(6分)
=450台.…(6分)(II)设从11月1日起,第n天的销售量最多,1≤n≤30,n∈N*
由(I),若商家在11月1日至15日之间未提价,则这15天家电M的总销售量为450台,
而450>414不符合题意,故n<15;
若n=5,则S15=5×2+
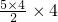 +10×16+
+10×16+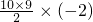 =120<414,
=120<414,也不符合题意,故n>5
因此,前n天每天的销售量组成一个首项为2,公差为4的等差数列,第n+1天开始每天的销售量组成首项为4n-4,
公差为-2的等差数列.…(10分)
∴S15=[2n+
 ]+[(15-n)(4n-4)+
]+[(15-n)(4n-4)+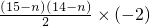 ]=-3n2+93n-270
]=-3n2+93n-270由已知条件,得S15=414,即-3n2+93n-270=414
解之得n=15或n=19(舍去19)
∴n=12,出售家电M的台数为2+11×4=46台
故在11月12日,该商场售出家电M的台数最多,这一天的销售量为46台.
分析:(I)由题意,在11月1日至15日之间该商场家电M每天的销售量组成公差为t的等差数列{an},结合等差数列的通项公式解出首项a1和公差t,从而由等差数列求和公式得到这15天家电M的总销售量.
(II)设从11月1日起,第n天的销售量最多(1≤n≤30,n∈N*).根据(I)前15天的销售量大于414,可得n<15;通过假设n=5算出销售量为120<414,得n>5.因此n为大于5而小于15的整数,因此结合题中数据列出S15关于n的式子,解方程S15=414,即可得到n=15,可得在11月12日,该商场售出家电M的台数最多,这一天的销售量为46台.
点评:本题给出商场家电的销售量成等差数列的模型,求家电M哪一天的销售量为最多.着重考查了函数、数列的基本知识及其应用能力,考查了函数方程思想和转化化归思想的应用,属于中档题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案
相关题目
某校高三(1)班50个学生选择选修模块课程,他们在A、B、C三个模块中进行选择,R至少需要选择l 个模块,具体模块选择的情况如下表:
| 模块 | 模块选择的学生人数 | 模块 | 模块选择的学生人数 |
| A | 28 | A与B | 11 |
| B | 26 | A与C | 12 |
| C | 26 | B与C | 13 |
- A.7
- B.6
- C.5
- D.4
 垂直
垂直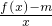 在(0,2)上是减函数,求实数m的取值范围.
在(0,2)上是减函数,求实数m的取值范围. 对称,则f(1)+f(2)+f(3)+f(4)+f(5)=______.
对称,则f(1)+f(2)+f(3)+f(4)+f(5)=______. ,则x的范围是 ________.
,则x的范围是 ________.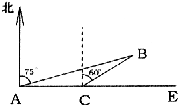 如图,海中有一小岛,周围3.8海里内有暗礁.一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北偏东60°.若此舰不改变舰行的方向继续前进,问此舰有没有触礁的危险?
如图,海中有一小岛,周围3.8海里内有暗礁.一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北偏东60°.若此舰不改变舰行的方向继续前进,问此舰有没有触礁的危险?