Question

已知函数．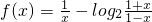
（1）试求函数f（x）的定义域，并判断函数f（x）的奇偶性；
（2）已知a是方程f（x）=0的一个实数解，求证：．

Answer 1

解：（1）由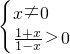得，x∈（-1，0）∪（0，1）
又∴f（x）为奇函数
（2）可证f（x）在（0，1）上是减函数，又f（x）为奇函数∴f（x）在（-1，0）上也是减函数

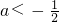∵，f（x）为奇函数∴或即

分析：（1）要使函数有意义，必须使得分母不为0，对数的真数大于0即可得函数的定义域，再利用f（-x）=-f（x），判断函数的奇偶性；
（2）易证函数在（0，1）上为减函数，在（-1，0）上也是减函数，又，问题可得证．
点评：本题主要考查函数的性质，考查定义域、单调性、奇偶性，属于基础题．