题目内容
已知函数 .
.(1)试求函数f(x)的单调区间;
(2)a>0,h(x)=ax2+2ax,g(x)=ex,若在(0,+∞)上至少存在一点x,使h(x)>g(x)成立,求实数a的取值范围.
【答案】分析:(1)先确定函数的定义域然后求导数fˊ(x),在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,求得的区间就是单调区间;
(2)欲在(0,+∞)上至少存在一点x,使h(x)>g(x)成立,只需f(x)= 的最大值大于1,建立不等关系,解之即可.
的最大值大于1,建立不等关系,解之即可.
解答:(1) (2分)
(2分)
若a<0,f(x)在 单调增,在
单调增,在 单调减
单调减
若a>0,f(x)在 单调增,在
单调增,在 单调减(5分)
单调减(5分)
(2)由(1)a>0时,f(x)在 增,
增, 减
减
要在(0,+∞)上存在一点x使h(x)>g(x)即f(x)>1
只须 ,即
,即 ,
, (13分)
(13分)
点评:本题主要考查了利用导数研究函数的单调性,以及函数的最值及其几何意义,属于基础题.
(2)欲在(0,+∞)上至少存在一点x,使h(x)>g(x)成立,只需f(x)=
 的最大值大于1,建立不等关系,解之即可.
的最大值大于1,建立不等关系,解之即可.解答:(1)
 (2分)
(2分)若a<0,f(x)在
 单调增,在
单调增,在 单调减
单调减若a>0,f(x)在
 单调增,在
单调增,在 单调减(5分)
单调减(5分)(2)由(1)a>0时,f(x)在
 增,
增, 减
减
要在(0,+∞)上存在一点x使h(x)>g(x)即f(x)>1
只须
 ,即
,即 ,
, (13分)
(13分)点评:本题主要考查了利用导数研究函数的单调性,以及函数的最值及其几何意义,属于基础题.

练习册系列答案
相关题目
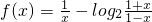 .
. .
. .
.