题目内容
(本小题13分)
已知函数![]() ,
,![]()
(1)试求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,若对
时,若对![]() ,都有
,都有![]() 成立,求实数b 的取值范围;
成立,求实数b 的取值范围;
(3)若![]() ,求证:
,求证:![]()
(1)![]() …………………2分
…………………2分
当a<2时, f(x)在![]() 和
和![]() 上递增,在
上递增,在![]() 上递减;
上递减;
当a=2时,f(x)在![]() 单调递增;
单调递增;
当a>2时,f(x)在![]() 和
和![]() 上递增,在
上递增,在![]() 上递减;……4分
上递减;……4分
(2)当![]() 时,由(1)知,
时,由(1)知,![]()
又![]() ,…………………………………6分
,…………………………………6分
∴![]() 在
在![]() 递增,在
递增,在![]() 上递减
上递减
∴![]() ………………………………………………8分
………………………………………………8分
由题意可知,![]() ,即
,即![]() ∴
∴![]() ………………9分
………………9分
(3)由(2)可知,函数![]() 在
在![]() 是减函数,
是减函数,
∴当![]() 时,有
时,有![]() ,
,![]() ,…11分
,…11分
即![]() ,
,![]() ,
,
两式相加,即得![]() ……………………………13分
……………………………13分

练习册系列答案
相关题目
 ,实数a,b为常数),
,实数a,b为常数), 在(0,+∞)上是单调增函数,求b的取值范围;
在(0,+∞)上是单调增函数,求b的取值范围; 在(0,1]上解的个数。
在(0,1]上解的个数。 .
. 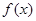 的最小正周期和当
的最小正周期和当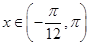 时的值域;
时的值域;
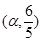 ,
,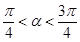 .求
.求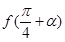 的值.
的值.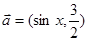 ,
,
 ∥
∥ 时,求
时,求 的值;
的值;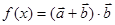 在
在 上的值域.
上的值域.