题目内容
设点A、B是抛物线y2=4px (p>0)上除原点O以外的两个动点,已知OA⊥OB,OM⊥AB,垂足为M,求点M的轨迹方程,并说明它表示什么曲线?
解 设直线OA的方程为y=kx (k≠±1,因为当k=±1时,直线AB的斜率不存在),则直线OB的方程为y=- ,
,

 将①②相乘,得y2+4pky=-x(x-4pk2),
将①②相乘,得y2+4pky=-x(x-4pk2),
即x2+y2=-4pky+4pk2x=4p(k2x-ky),③
又k2x-ky=x,代入③式并化简,
得(x-2p)2+y2=4p2.
当k=±1时,易求得直线AB的方程为x=4p.
故此时点M的坐标为(4p,0),也在(x-2p)2+y2=4p2 (x≠0)上.
∴点M的轨迹方程为(x-2p)2+y2=4p2 (x≠0),
∴其轨迹是以(2p,0)为圆心,半径为2p的圆,去掉坐标原点.

练习册系列答案
相关题目
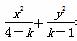 =1,给出下面四个命题:
=1,给出下面四个命题: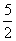 .
.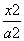 +
+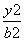 =1 (a>b>0)的焦距为2,以O为圆心,a为半径
=1 (a>b>0)的焦距为2,以O为圆心,a为半径 作圆,过点
作圆,过点 作圆的两切线互相垂直,则离心率e=________.
作圆的两切线互相垂直,则离心率e=________. +
+ =1长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF.求点P的坐标.
=1长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF.求点P的坐标. 的否定是( )
的否定是( ) B.
B.
 D.
D.
 -log2x,在下列区间中,则f(x)的零点所在的区间是( )
-log2x,在下列区间中,则f(x)的零点所在的区间是( ) ,则“
,则“ ”是“
”是“ ”的
”的  的半径为2,
的半径为2,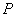 是圆
是圆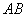 延长线上的一点,
延长线上的一点, =1,割线
=1,割线 交圆
交圆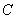 、
、 两点,过
两点,过 ,交直线
,交直线 于点
于点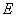 ,交直线
,交直线 于点
于点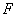 .
. ;
; 的值.
的值.