题目内容
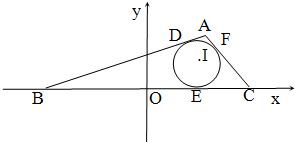 如图,△ABC的内切圆与三边AB、BC、CA的切点分别为D、E、F,已知B(-
如图,△ABC的内切圆与三边AB、BC、CA的切点分别为D、E、F,已知B(-| 2 |
| 2 |
(1)求L的方程;
(2)过点C作直线m交曲线L于不同的两点M、N,问在x轴上是否存在一个异于点C的定点Q.使
| ||||
|
|
| ||||
|
|
分析:(1)由切线长定理得,从一点出发的切线长相等,得到A点到两个点B,C的距离之差是常数,根据双曲线的定义得A点的轨迹是双曲线,从而即可求出L的方程;
(2)对于存在性问题,可先假设存在,设点Q(x0,0),再设M(x1,y1),N(x2,y2),由条件得∠MQC=∠NQC,下面分类讨论:①当MN⊥x,②当MN不垂直x时,第一种情况比较简单,对于第二种情况,将直线的方程代入双曲线方程,消去y得到关于x的二次方程,结合根与系数的关系,利用斜率相等求得Q(
,0),从而说明存在点Q.
(2)对于存在性问题,可先假设存在,设点Q(x0,0),再设M(x1,y1),N(x2,y2),由条件得∠MQC=∠NQC,下面分类讨论:①当MN⊥x,②当MN不垂直x时,第一种情况比较简单,对于第二种情况,将直线的方程代入双曲线方程,消去y得到关于x的二次方程,结合根与系数的关系,利用斜率相等求得Q(
| ||
| 2 |
解答:解:(1)由题意|AD|=|AF|.|BD|=|BE|,|CE|=|CF|.
∴|AB|-|AC|=|BD|-|CF|=|BE|-|CE|=|BO|+|OE|-(|OC|-|OE|)=2|OE|
I(1,t),E(1,0),|OE|=1,|AB|-|AC|=2
x2-y2=1(x>1)
(2)设点Q(x0,0),设M(x1,y1),N(x2,y2)
∵
=
?
=
?cos<
,
=cos<
,
?∠MQC=∠NQC
(6分)
于是:①当MN⊥x,点Q(x0,0)在x上任何一点处,都能够使得:
∠MQC=∠NQC成立,(8分)
②当MN不垂直x时,设直线MN:y=k(x-
).
由
得:(1-k2)x2+2
k2x-(2k2+1)=0
则:x1+x2=
,x1x2=
∴y1+y2=k(x1-
)+k(x2-
)=k(x1+x2)-2
k =
∵tan∠MQC=kQM=
,tan∠NQC=-kQN=-
要使∠MQC=∠NQC成立,
只要tan∠MQC=tan∠NQC:
=-
?x2y1-x0y1+x1y2-x0y2=0
即(y1+y2)x0=x2•k(x1-
)+x1•k(x2-
)=2kx1x2-
k(x1+x2)=
∴
•x0=
?x0=
∴当Q(
,0)时,能够使:
=
对任意的直线m成立.(15分)
∴|AB|-|AC|=|BD|-|CF|=|BE|-|CE|=|BO|+|OE|-(|OC|-|OE|)=2|OE|
I(1,t),E(1,0),|OE|=1,|AB|-|AC|=2
x2-y2=1(x>1)
(2)设点Q(x0,0),设M(x1,y1),N(x2,y2)
∵
| ||||
|
|
| ||||
|
|
| ||||
|
|
| ||||
|
|
| QM |
| QC |
| QN |
| QC |
(6分)
于是:①当MN⊥x,点Q(x0,0)在x上任何一点处,都能够使得:
∠MQC=∠NQC成立,(8分)
②当MN不垂直x时,设直线MN:y=k(x-
| 2 |
由
|
| 2 |
则:x1+x2=
2
| ||
| k2-1 |
| 2k2+1 |
| k2-1 |
∴y1+y2=k(x1-
| 2 |
| 2 |
| 2 |
2
| ||
| k2-1 |
∵tan∠MQC=kQM=
| y1 |
| x1-x0 |
| y2 |
| x2-x0 |
只要tan∠MQC=tan∠NQC:
| y1 |
| x1-x0 |
| y2 |
| x2-x0 |
即(y1+y2)x0=x2•k(x1-
| 2 |
| 2 |
| 2 |
| 2k |
| k2-1 |
∴
2
| ||
| k2-1 |
| 2k |
| k2-1 |
| ||
| 2 |
| ||
| 2 |
| ||||
|
|
| ||||
|
|
点评:本题主要考查了轨迹方程、直线与圆锥曲线的交点等知识,属于中档题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
 11、如图,△ABC是圆的内接三角形,PA切圆于点A,PB交圆于点D.若∠ABC=60°,PD=1,BD=8,则∠PAC=
11、如图,△ABC是圆的内接三角形,PA切圆于点A,PB交圆于点D.若∠ABC=60°,PD=1,BD=8,则∠PAC=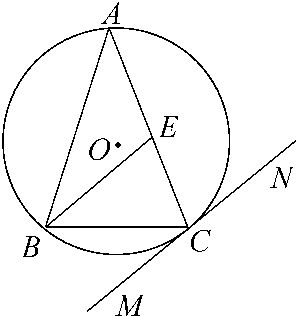 如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E.若AB=6,BC=4,求AE的长.
如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E.若AB=6,BC=4,求AE的长.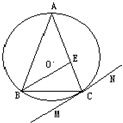 (1)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线
(1)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线 如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E.若AB=6,BC=4,则AE的长为
如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E.若AB=6,BC=4,则AE的长为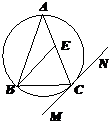 如图:△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E,若AB=6,BC=4,则AE的长为( )
如图:△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E,若AB=6,BC=4,则AE的长为( )