题目内容
记直线 x=π,y=π 与两个坐标轴所围成的区域内的点为(a,b),则函数f(x)=x2+2ax+π2-b2有零点的概率为( )
分析:根据函数f(x)=x2+2ax+π2-b2有零点,利用根的判别式算出a2+b2≥π2.由此作出如图所示直角坐标系,可得满足条件的点(a,b)在正方形内圆外的部分,即如图的阴影部分区域.由此利用面积计算公式和几何概型公式加以计算,可得所求的概率.
解答:解:若函数f(x)=x2+2ax+π2-b2有零点,
则△=(2a)2-4(π2-b2)≥0,即a2+b2≥π2.
在坐标轴上将a,b的取值范围标出,如图所示
当a、b满足函数有零点时,点(a,b)位于正方形OABC内且在圆外的部分,即如图的阴影部分区域.
∵正方形OABC面积为S1=π2,扇形OAC面积为S2=
π•OA2=
,
∴阴影部分面积为S=S1-S2=π2(1-
),
因此可得函数f(x)=x2+2ax+π2-b2有零点的概率为:
P=
=
=1-
.
故选:D

则△=(2a)2-4(π2-b2)≥0,即a2+b2≥π2.
在坐标轴上将a,b的取值范围标出,如图所示
当a、b满足函数有零点时,点(a,b)位于正方形OABC内且在圆外的部分,即如图的阴影部分区域.
∵正方形OABC面积为S1=π2,扇形OAC面积为S2=
| 1 |
| 4 |
| π3 |
| 4 |
∴阴影部分面积为S=S1-S2=π2(1-
| π |
| 4 |
因此可得函数f(x)=x2+2ax+π2-b2有零点的概率为:
P=
| S |
| S1 |
π2(1-
| ||
| π2 |
| π |
| 4 |
故选:D
点评:本题给出二次函数有零点,求相应的概率,着重考查了一元二次方程根与系数的关系、面积计算公式和几何概型的计算等知识,属于中档题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
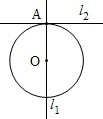 (2013•江西)如图.已知l1⊥l2,圆心在l1上、半径为1m的圆O在t=0时与l2相切于点A,圆O沿l1以1m/s的速度匀速向上移动,圆被直线l2所截上方圆弧长记为x,令y=cosx,则y与时间t(0≤t≤1,单位:s)的函数y=f(t)的图象大致为( )
(2013•江西)如图.已知l1⊥l2,圆心在l1上、半径为1m的圆O在t=0时与l2相切于点A,圆O沿l1以1m/s的速度匀速向上移动,圆被直线l2所截上方圆弧长记为x,令y=cosx,则y与时间t(0≤t≤1,单位:s)的函数y=f(t)的图象大致为( )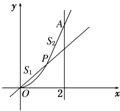 如图,设点P从原点沿曲线y=x2向点A(2,4)移动,记直线OP、曲线y=x2及直线x=2所围成的面积分别记为S1,S2,若S1=S2,则点P的坐标为
如图,设点P从原点沿曲线y=x2向点A(2,4)移动,记直线OP、曲线y=x2及直线x=2所围成的面积分别记为S1,S2,若S1=S2,则点P的坐标为