题目内容
已知一扇形的中心角是α,所在圆的半径为R.(1)若α=60°,R=10 cm,求扇形的弧长及该弧所在的弓形的面积.
(2)若扇形的周长是一定值C(C>0),问当α为多少弧度时,该扇形的面积有最大值?并求出这个最大值.
思路点拨:本题可以直接根据弧长公式与扇形面积公式进行解答.
解:(1)设弧长为l,弓形面积记作S弓.
由α=60°=![]() ,R=10,得
,R=10,得
l=|α|·R=![]() (cm),
(cm),
S弓=S扇形-S三角形=![]() l·R-
l·R-![]() R2sinα
R2sinα
=![]() ×
×![]() ×10-
×10-![]() ×102×sin
×102×sin![]()
=50(![]() -
-![]() )(cm2).
)(cm2).
(2)∵扇形周长C=2R+l=2R+|α|·R,
∴R=![]() .
.
∴S扇形=![]() |α|·R2=
|α|·R2=![]() |α|(
|α|(![]() )2=
)2=![]() ×|α|×
×|α|×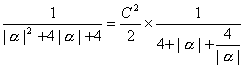 ≤
≤![]() .
.
∴当且仅当|α|=![]() 时,即α=2(α=-2舍去)时,扇形面积有最大值
时,即α=2(α=-2舍去)时,扇形面积有最大值![]() .
.
[一通百通] 此类问题是将三角函数问题与不等式问题进行综合考查的.扇形面积与弧长的计算是立体几何中研究折线问题的基础,在计算扇形的弧长与面积计算公式时都有角度制与弧度制两种给出方式,其中用弧度制不仅形式易记,而且使用方便,在使用时注意要把角度都换成弧度,使度量单位一致.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
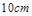 ,当扇形的圆心角a为多少弧度时,该扇形面积有最大面积 ?
,当扇形的圆心角a为多少弧度时,该扇形面积有最大面积 ?