题目内容
18.若数列{an}满足:an+1+(-1)nan=n(n∈N*),则a1+a2+…+a100=2550.分析 an+1+(-1)nan=n(n∈N*),可得:a2-a1=1,a3+a2=2,a4-a3=3,a5+a4=4,a6-a5=5,a7+a6=6,a8-a7=7,…,可得a3+a1=1=a7+a5=…,a4+a2=2+3,a8+a6=6+7,a12+a10=10+11,…,利用分组求和即可得出.
解答 解:∵an+1+(-1)nan=n(n∈N*),
∴a2-a1=1,a3+a2=2,a4-a3=3,a5+a4=4,a6-a5=5,a7+a6=6,a8-a7=7,…,
可得a3+a1=1=a7+a5=…,∴(a1+a3+…+a99)=25.
a4+a2=2+3,a8+a6=6+7,a12+a10=10+11,…,∴a2+a4+…+a100=5×25+8×$\frac{25×24}{2}$=2525.
则a1+a2+…+a100=2550.
故答案为:2550.
点评 本题考查了等差数列的通项公式及其前n项和公式、递推关系、分组求和,考查了分类讨论方法、推理能力与计算能力,属于难题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
8.若非空集合A={x|a+1≤x≤3a-5},集合B={x|1≤x≤16},则满足A⊆(A∩B)的实数a的取值范围是( )
| A. | [0,7] | B. | [7,15] | C. | [3,7] | D. | [3,15] |
6.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点为F1,P为左支上一点,|PF1|=a,P0与P关于原点对称,且$\overrightarrow{{P}_{0}{F}_{1}}$$•\overrightarrow{P{F}_{1}}$=0.则双曲线的渐近线方程为( )
| A. | y=±x | B. | y=$±\frac{\sqrt{6}}{2}$x | C. | y=$±\frac{\sqrt{3}}{2}$x | D. | y=±2x |
13.关于三个不同平面α,β,γ与直线l,下列命题中的假命题是( )
| A. | 若α⊥β,则α内一定存在直线平行于β | |
| B. | 若α与β不垂直,则α内一定不存在直线垂直于β | |
| C. | 若α⊥γ,β⊥γ,α∩β=l,则l⊥γ | |
| D. | 若α⊥β,则α内所有直线垂直于β |
8.已知α,β为锐角,且cos(α+β)=$\frac{3}{5}$,sinα=$\frac{5}{13}$,则cosβ的值为( )
| A. | $\frac{56}{65}$ | B. | $\frac{33}{65}$ | C. | $\frac{16}{65}$ | D. | $\frac{63}{65}$ |
 某地区交管部门为了对该地区驾驶员的某项考试成绩进行分析,随机抽取了15分到45分之间的1000名学员的成绩,并根据这1000名驾驶员的成绩画出样本的频率分布直方图(如图),则成绩在[30,35)内的驾驶员人数共有300.
某地区交管部门为了对该地区驾驶员的某项考试成绩进行分析,随机抽取了15分到45分之间的1000名学员的成绩,并根据这1000名驾驶员的成绩画出样本的频率分布直方图(如图),则成绩在[30,35)内的驾驶员人数共有300.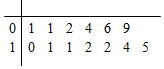
 给出下列命题:
给出下列命题: