题目内容
设Sn是数列{an}的前n项和，已知a1=1，an=-Sn•Sn-1（n≥2），则Sn=
- A.n2
- B.
- C.n
- D.
D
分析：当n≥2时，an=Sn-Sn-1，与已知结合，可知{
}为等差数列，从而可求得答案．
解答：∵当n≥2时，an=Sn-Sn-1，又an=-Sn•Sn-1（n≥2），
∴Sn-Sn-1=-Sn•Sn-1（n≥2），
∴-
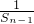=1（n≥2），又
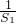=1，
∴{}是首项为1，公差为1的等差数列，
∴=1+（n-1）×1=n．
∴Sn=．
故选D．
点评：本题考查数列的求和，分析得到{}为等差数列是关键，也是难点，考查转化与分析运算能力，属于中档题．
分析：当n≥2时，an=Sn-Sn-1，与已知结合，可知{
}为等差数列，从而可求得答案．解答：∵当n≥2时，an=Sn-Sn-1，又an=-Sn•Sn-1（n≥2），
∴Sn-Sn-1=-Sn•Sn-1（n≥2），
∴
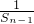-=1（n≥2），又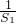=1，∴{
}是首项为1，公差为1的等差数列，∴
=1+（n-1）×1=n．∴Sn=
．故选D．
点评：本题考查数列的求和，分析得到{
}为等差数列是关键，也是难点，考查转化与分析运算能力，属于中档题． 
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目