题目内容
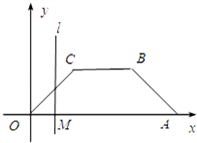
如 图,梯形OABC各顶点的坐标分别为O(0,0),A(6,0),B(4,2),C(2,2).一条与y轴平行的动直线l从点O开始作平行移动,到点A停止,设直线l与x轴的交点为M,OM=x,梯形被直线l截得的在l左侧的图形的面积为y,求函数y=f(x)的解析式、定义域、值域以及f[f(
图,梯形OABC各顶点的坐标分别为O(0,0),A(6,0),B(4,2),C(2,2).一条与y轴平行的动直线l从点O开始作平行移动,到点A停止,设直线l与x轴的交点为M,OM=x,梯形被直线l截得的在l左侧的图形的面积为y,求函数y=f(x)的解析式、定义域、值域以及f[f(
)]的值.
 图,梯形OABC各顶点的坐标分别为O(0,0),A(6,0),B(4,2),C(2,2).一条与y轴平行的动直线l从点O开始作平行移动,到点A停止,设直线l与x轴的交点为M,OM=x,梯形被直线l截得的在l左侧的图形的面积为y,求函数y=f(x)的解析式、定义域、值域以及f[f(
图,梯形OABC各顶点的坐标分别为O(0,0),A(6,0),B(4,2),C(2,2).一条与y轴平行的动直线l从点O开始作平行移动,到点A停止,设直线l与x轴的交点为M,OM=x,梯形被直线l截得的在l左侧的图形的面积为y,求函数y=f(x)的解析式、定义域、值域以及f[f(| 7 | 2 |
分析:将点M分在三段中分别根据梯形被直线l截得的在l左侧的图形的形状求出相应的面积,得到面积函数,求出定义域和值域,最后根据解析式可求出f[f(
)]的值.
| 7 |
| 2 |
解答:解:当x∈[0,2)时,l左侧的图形是等腰直角三角形,其面积为y=
x2;
当x∈(2,4]时,l左侧的图形是直角梯形,其面积为y=2+2(x-2)=2x-2;
当x∈(4,6]时,l左侧的图形是梯形减去一个等腰直角三角形,其面积为y=
+
(x-4)2=-
x2+6x-10
∴f(x)=
,定义域[0,6],值域[0,8];
∴f[f(
)]=f(5)=
.
| 1 |
| 2 |
当x∈(2,4]时,l左侧的图形是直角梯形,其面积为y=2+2(x-2)=2x-2;
当x∈(4,6]时,l左侧的图形是梯形减去一个等腰直角三角形,其面积为y=
| 2(2+4) |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴f(x)=
|
∴f[f(
| 7 |
| 2 |
| 15 |
| 2 |
点评:本题主要考查了分段函数的应用,以及函数的值域和定义域的求解,同时考查了运算求解的能力和识图能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
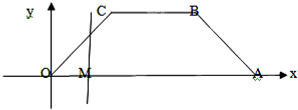 如图,等腰梯形OABC,底角为45°,各顶点的坐标分别为O(0,0),A(6,0),B(4,2),C(2,2).一条与y轴平行的动直线l从O点开始做平行移动,到A点为止.设直线l与x轴的交点M,记OM=x,记梯形被直线l截得的在l左侧的图形面积为y.
如图,等腰梯形OABC,底角为45°,各顶点的坐标分别为O(0,0),A(6,0),B(4,2),C(2,2).一条与y轴平行的动直线l从O点开始做平行移动,到A点为止.设直线l与x轴的交点M,记OM=x,记梯形被直线l截得的在l左侧的图形面积为y.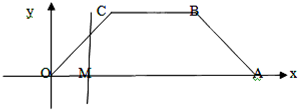 如图,等腰梯形OABC,底角为45°,各顶点的坐标分别为O(0,0),A(6,0),B(4,2),C(2,2).一条与y轴平行的动直线l从O点开始做平行移动,到A点为止.设直线l与x轴的交点M,记OM=x,记梯形被直线l截得的在l左侧的图形面积为y.
如图,等腰梯形OABC,底角为45°,各顶点的坐标分别为O(0,0),A(6,0),B(4,2),C(2,2).一条与y轴平行的动直线l从O点开始做平行移动,到A点为止.设直线l与x轴的交点M,记OM=x,记梯形被直线l截得的在l左侧的图形面积为y. )]的值.
)]的值. 图,梯形OABC各顶点的坐标分别为O(0,0),A(6,0),B(4,2),C(2,2).一条与y轴平行的动直线l从点O开始作平行移动,到点A停止,设直线l与x轴的交点为M,OM=x,梯形被直线l截得的在l左侧的图形的面积为y,求函数y=f(x)的解析式、定义域、值域以及
图,梯形OABC各顶点的坐标分别为O(0,0),A(6,0),B(4,2),C(2,2).一条与y轴平行的动直线l从点O开始作平行移动,到点A停止,设直线l与x轴的交点为M,OM=x,梯形被直线l截得的在l左侧的图形的面积为y,求函数y=f(x)的解析式、定义域、值域以及 的值.
的值.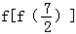 的值.
的值.