题目内容
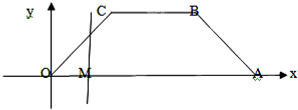 如图,等腰梯形OABC,底角为45°,各顶点的坐标分别为O(0,0),A(6,0),B(4,2),C(2,2).一条与y轴平行的动直线l从O点开始做平行移动,到A点为止.设直线l与x轴的交点M,记OM=x,记梯形被直线l截得的在l左侧的图形面积为y.
如图,等腰梯形OABC,底角为45°,各顶点的坐标分别为O(0,0),A(6,0),B(4,2),C(2,2).一条与y轴平行的动直线l从O点开始做平行移动,到A点为止.设直线l与x轴的交点M,记OM=x,记梯形被直线l截得的在l左侧的图形面积为y.(1)函数y=f(x)的解析式;
(2)求函数的定义域、值域;
(3)计算[f(
| 7 | 2 |
分析:(1)分直线l从O运动到C,从C运动到B,从B运动到A三种情况写出对应图形的面积,所以函数为分段函数;
(2)分段求出各部分的值域,取并集;
(3)根据
所在的区间代入相应的解析式求解.
(2)分段求出各部分的值域,取并集;
(3)根据
| 7 |
| 2 |
解答:解:(1)当0≤x≤2,y=
x2,
当2<x≤4时,y=
×2×2+2×(x-2)=2x-2.
当4<x≤6时,y=
×2×2+2×2+
×2×2-
(6-x)2=-
x2+6x-10.
所以f(x)=
(2)函数定义域为[0,6],
当0≤x≤2时,y=
x2∈[0,2];
当2<x≤4时,y=2x-2∈(2,6];
当4<x≤6时,y=-
x2+6x-10∈(6,8],
所以函数值域为[0,8].
(3)f(
)=2×
-2=5.
| 1 |
| 2 |
当2<x≤4时,y=
| 1 |
| 2 |
当4<x≤6时,y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以f(x)=
|
(2)函数定义域为[0,6],
当0≤x≤2时,y=
| 1 |
| 2 |
当2<x≤4时,y=2x-2∈(2,6];
当4<x≤6时,y=-
| 1 |
| 2 |
所以函数值域为[0,8].
(3)f(
| 7 |
| 2 |
| 7 |
| 2 |
点评:本题考查了实际背景下的分段函数解析式的求解方法,解答的关键是根据变量在不同的区间段列不同的解析式,同时注意分段函数的定义域和值域都是各段的并集.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•泉州模拟)如图,等腰梯形ABCD中,AB∥CD且AB=2,AD=1,DC=2x(x∈(0,1)).以A,B为焦点,且过点D的双曲线的离心率为e1;以C,D为焦点,且过点A的椭圆的离心率为e2,则e1+e2的取值范围为 ( )
(2013•泉州模拟)如图,等腰梯形ABCD中,AB∥CD且AB=2,AD=1,DC=2x(x∈(0,1)).以A,B为焦点,且过点D的双曲线的离心率为e1;以C,D为焦点,且过点A的椭圆的离心率为e2,则e1+e2的取值范围为 ( ) 如图,直角梯形OABC位于直线x=t(0≤t≤5)右侧的图形面积为f(t).
如图,直角梯形OABC位于直线x=t(0≤t≤5)右侧的图形面积为f(t).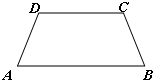 (2013•长春一模)如图,等腰梯形ABCD中,AB∥CD且AB=2AD,
(2013•长春一模)如图,等腰梯形ABCD中,AB∥CD且AB=2AD,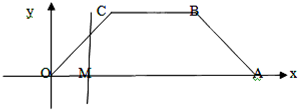 如图,等腰梯形OABC,底角为45°,各顶点的坐标分别为O(0,0),A(6,0),B(4,2),C(2,2).一条与y轴平行的动直线l从O点开始做平行移动,到A点为止.设直线l与x轴的交点M,记OM=x,记梯形被直线l截得的在l左侧的图形面积为y.
如图,等腰梯形OABC,底角为45°,各顶点的坐标分别为O(0,0),A(6,0),B(4,2),C(2,2).一条与y轴平行的动直线l从O点开始做平行移动,到A点为止.设直线l与x轴的交点M,记OM=x,记梯形被直线l截得的在l左侧的图形面积为y. )]的值.
)]的值.