题目内容
在某海域中,直径为30海里的暗礁区中心有一哨所,值班人员发现有一轮船从哨所正西方向45海里的B处向哨所驶来,哨所及时向轮船发出危险信号,但轮船没有收到信号,又继续前进了15海里到达C处才收到此哨所第二次发出的紧急危险信号.
(1)若轮船收到第一次危险信号后,为避免触礁,航向改变角度至少应为东偏北多少度?
(2)当轮船收到第二次危险信号时,为避免触礁,轮船航向改变的角度至少应为东偏南多少度?(精确到度)
答案:
解析:
解析:
|
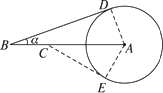
解:(1)过B作⊙A的切线,D为切点,连结DA,则∠ADB=90°. 在Rt△ABD中,sinα= 所以α≈20°. (2)过C作⊙A的切线,E为切点,连结AE,则∠AEC=90°. 在Rt△ACE中,AC=45-15=30(海里), sin∠ACE= 所以∠ACE=30°. 分析:轮船是否有触礁危险,在于轮船航行所在的直线与以A点为圆心、以15海里为半径的圆的位置关系,此题应从直线与圆相切这一特殊位置关系入手.触礁问题是传统的三角应用题,综合了解直角三角形、直线与圆的位置关系、切线的性质与判定等知识,解此题时要注意切线的作用.
|

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
某中学共有1000名学生参加了该地区高三第一次质量检测的数学考试,数学成绩如下表所示:
(I)为了了解同学们前段复习的得失,以便制定下阶段的复习计划,学校将采用分层抽样的方法抽取100名同学进行问卷调查,甲同学在本次测试中数学成绩为95分,求他被抽中的概率;
(II)已知本次数学成绩的优秀线为110分,试根据所提供数据估计该中学达到优秀线的人数;
(III)作出频率分布直方图,并估计该学校本次考试的数学平均分.(同一组中的数据用该组区间的中点值作代表)
| 数学成绩分组 | [0,30) | [30,60) | [60,90) | [90,120) | [120,150] |
| 人数 | 60 | 90 | 300 | x | 160 |
(II)已知本次数学成绩的优秀线为110分,试根据所提供数据估计该中学达到优秀线的人数;
(III)作出频率分布直方图,并估计该学校本次考试的数学平均分.(同一组中的数据用该组区间的中点值作代表)
 如图,某海域中有甲、乙两艘测量船分别停留在相距(
如图,某海域中有甲、乙两艘测量船分别停留在相距(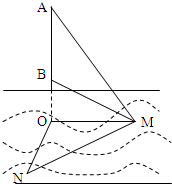 如图,某海域中有甲、乙两艘测量船分别停留在相距(
如图,某海域中有甲、乙两艘测量船分别停留在相距(
 )海里的M,N两地,他们在同时观测岛屿上中国移动信号塔AB,设塔底延长线与海平面交于点O.已知点M在点O的正东方向,点N在点O的南偏西15°方向,ON=
)海里的M,N两地,他们在同时观测岛屿上中国移动信号塔AB,设塔底延长线与海平面交于点O.已知点M在点O的正东方向,点N在点O的南偏西15°方向,ON= 海里,在M处测得塔底B和塔顶A的仰角分别为30°和60°.
海里,在M处测得塔底B和塔顶A的仰角分别为30°和60°.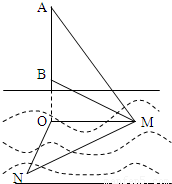 如图,某海域中有甲、乙两艘测量船分别停留在相距(
如图,某海域中有甲、乙两艘测量船分别停留在相距(
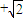 )海里的M,N两地,他们在同时观测岛屿上中国移动信号塔AB,设塔底延长线与海平面交于点O.已知点M在点O的正东方向,点N在点O的南偏西15°方向,ON=2
)海里的M,N两地,他们在同时观测岛屿上中国移动信号塔AB,设塔底延长线与海平面交于点O.已知点M在点O的正东方向,点N在点O的南偏西15°方向,ON=2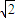 海里,在M处测得塔底B和塔顶A的仰角分别为30°和60°.
海里,在M处测得塔底B和塔顶A的仰角分别为30°和60°.