题目内容
 如图,某海域中有甲、乙两艘测量船分别停留在相距(
如图,某海域中有甲、乙两艘测量船分别停留在相距(| 6 |
| 2 |
| 2 |
(1)求信号塔AB的高度;
(2)乙船试图在线段ON上选取一点P,使得在点P处观测信号塔AB的视角最大,请判断这样的点P是否存在,若存在,求出最大视角及OP的长;若不存在,说明理由.
分析:(1)由条件可得∠MON=105°,在△MON中,由正弦定理求得sin∠OMN=
,∠OMN=45°,可得∠ONM=30°.再由正弦定理求得OM 的值,解直角三角形求出OA和OB的值,可得AB的值.
(2)假设存在符合条件的点P,令OP=x,0<x≤2
,设∠OPA=α,∠OPB=β,可得视角θ=α-β,tanα 和 tanβ 的解析式,再由tanθ=tan(α-β),利用两角差的正切公式求出tanθ的最大值,并求出此时x的值.
| ||
| 2 |
(2)假设存在符合条件的点P,令OP=x,0<x≤2
| 2 |
解答:解:(1)由条件可得∠MON=105°,在△MON中,由正弦定理可得
=
,
即
=
,解得 sin∠OMN=
,∠OMN=45°,∴∠ONM=30°.
再由
=
求得OM=2.
∵在M处测得塔底B和塔顶A的仰角分别为30°和60°,∴OB=
=
,OA=2
,∴AB=
,
即信号塔AB的高度为
海里.
(2)假设存在符合条件的点P,令OP=x,0<x≤2
,设∠OPA=α,∠OPB=β,
∴视角θ=α-β,tanα=
,tanβ=
.
∴tanθ=tan(α-β)=
=
×
.
由于x>0,∴x+
≥2
=4,当且仅当x=2时,等号成立,故tanθ≤
.
综上可得,满足条件的点P存在.
| MN |
| sin∠MON |
| ON |
| sin∠OMN |
即
| ||||
| sin105° |
2
| ||
| sin∠OMN |
| ||
| 2 |
再由
| OM |
| sin∠ONM |
| ON |
| sin∠OMN |
∵在M处测得塔底B和塔顶A的仰角分别为30°和60°,∴OB=
| 2 | ||
|
2
| ||
| 3 |
| 3 |
4
| ||
| 3 |
即信号塔AB的高度为
4
| ||
| 3 |
(2)假设存在符合条件的点P,令OP=x,0<x≤2
| 2 |
∴视角θ=α-β,tanα=
2
| ||
| x |
2
| ||
| 3x |
∴tanθ=tan(α-β)=
| tanα-tanβ |
| 1+tanα•tanβ |
4
| ||
| 3 |
| 1 | ||
x+
|
由于x>0,∴x+
| 4 |
| x |
x•
|
| ||
| 3 |
综上可得,满足条件的点P存在.
点评:本题主要考查正弦定理的应用,两角差的正切公式、基本不等式的应用,属于中档题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
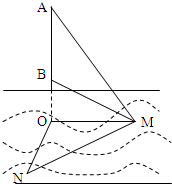 如图,某海域中有甲、乙两艘测量船分别停留在相距(
如图,某海域中有甲、乙两艘测量船分别停留在相距(
 )海里的M,N两地,他们在同时观测岛屿上中国移动信号塔AB,设塔底延长线与海平面交于点O.已知点M在点O的正东方向,点N在点O的南偏西15°方向,ON=
)海里的M,N两地,他们在同时观测岛屿上中国移动信号塔AB,设塔底延长线与海平面交于点O.已知点M在点O的正东方向,点N在点O的南偏西15°方向,ON= 海里,在M处测得塔底B和塔顶A的仰角分别为30°和60°.
海里,在M处测得塔底B和塔顶A的仰角分别为30°和60°.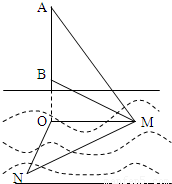 如图,某海域中有甲、乙两艘测量船分别停留在相距(
如图,某海域中有甲、乙两艘测量船分别停留在相距(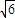
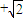 )海里的M,N两地,他们在同时观测岛屿上中国移动信号塔AB,设塔底延长线与海平面交于点O.已知点M在点O的正东方向,点N在点O的南偏西15°方向,ON=2
)海里的M,N两地,他们在同时观测岛屿上中国移动信号塔AB,设塔底延长线与海平面交于点O.已知点M在点O的正东方向,点N在点O的南偏西15°方向,ON=2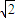 海里,在M处测得塔底B和塔顶A的仰角分别为30°和60°.
海里,在M处测得塔底B和塔顶A的仰角分别为30°和60°.