题目内容
设f(x)=ax3+bx+c(a≠0)为奇函数,其图象在点(1,f(1))处的切线与直线x-6y-7=0垂直,导函数f′(x)的最小值为-12.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调增区间,并求函数f(x)在[-1,3]上的最大值和最小值.
解:(1)∵f(x)为奇函数,∴f(-x)=-f(x)
即-ax3-bx+c=-ax3-bx-c,∴c=0.
又f′(x)=3ax2+b的最小值为-12,∴b=-12.
由题设知f′(1)=3a+b=-6,∴a=2,
故f(x)=2x3-12x.
(2) f′(x)=6x2-12=6(x+ )(x-
)(x- )
)
当x变化时,f′(x)、f(x)的变化情况表如下:
| x | (-∞,- | - | (- |
| ( |
| f′(x) | + | 0 | - | 0 | + |
| f(x) |
| 极大值 |
| 极小值 |
|

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目



 的离心率是
的离心率是 ,则
,则 的值为 .
的值为 . 中,直线l的参数方程为
中,直线l的参数方程为 . 以直角坐标系xOy中的原点O为极点,x轴的非负半轴为极轴,圆C的极坐标方程为
. 以直角坐标系xOy中的原点O为极点,x轴的非负半轴为极轴,圆C的极坐标方程为 ,则圆心C到直线l距离为
,则圆心C到直线l距离为 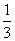 x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)的图象,则f(-1)等于( ).
x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)的图象,则f(-1)等于( ).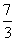 D.-
D.-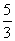
 bx2+cx(c<0),其图象在点A(1,0)处的切线的斜率为0,则f(x)的单调递增区间是________.
bx2+cx(c<0),其图象在点A(1,0)处的切线的斜率为0,则f(x)的单调递增区间是________.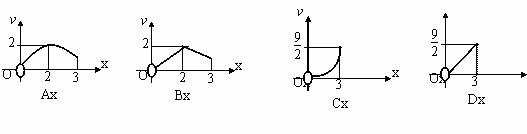
 ( ),
( ), C.9 D.
C.9 D.
 的前n项和为
的前n项和为 ,已知
,已知 则数列
则数列 C.
C.  D.
D.