题目内容
数列{an}中,a1=0,对任意n≥2且n∈N*时{an}的各项为正值,an+1(an+1-2)=4an(an+1),bn=log2(an+2)都成立.(1)求数列{an}、{bn}的通项公式;
(2)当k＞3且k∈N*时,证明对任意n∈N*都有
+
+
+…+
＞1成立.
（1）解:由an+1(an+1-2)=4an(an+1)，得
(an+1+2an)(an+1-2an-2)=0.
数列{an}的各项为正值,an+1+2an＞0,
∴an+1=2an+2.∴an+1+2=2(an+2).
又a1+2=2≠0,
∴数列{an+2}为等比数列.
∴an+2=(a1+2)·2n-1=2n,an=2n-2,即为数列{an}的通项公式.
bn=log2(2n-2+2)=n.
(2)证明:设S=+++…+=
+
+
+…+
, ①
∴2S=(
+
)+(
+
)+(
+
)+…+(
+
).
当x＞0,y＞0时,x+y≥2
,
+
≥2
,
∴(x+y)(
+
)≥4.
∴
+
≥
,当且仅当x=y时等号成立.
上述①式中,k＞3,n＞0,n+1,n+2,…,nk-1全为正,
∴2S＞
+
+…+
.
∴S＞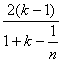
＞
=2(1-
)＞2(1-
)=1,得证.
练习册系列答案
全能测控期末小状元系列答案
相关题目