题目内容
已知向量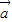 =(
=( cosx,0),
cosx,0),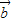 =(0,sinx).记函数f(x)=(
=(0,sinx).记函数f(x)=(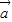 +
+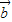 )2十
)2十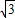 sin2x.
sin2x.(I)求函数f(x)的最小值及取最小值时x的集合;
(II)求函数f (x)的单调递增区间.
【答案】分析:(1)根据平面向量的坐标运算得( +
+ )2=1+2cos2x,再结合二倍角的余弦公式和辅助角公式化简,得到f(x)=2sin(2x+
)2=1+2cos2x,再结合二倍角的余弦公式和辅助角公式化简,得到f(x)=2sin(2x+ )+2,最后根据正弦函数最值的结论,可得f(x)的最小值及取最小值时x的集合;
)+2,最后根据正弦函数最值的结论,可得f(x)的最小值及取最小值时x的集合;
(2)根据(1)化简得的表达式,列出不等式- +2kπ≤2x+
+2kπ≤2x+ ≤
≤ +2kπ(k∈Z),解此不等式再将它变成区间,即可得到
+2kπ(k∈Z),解此不等式再将它变成区间,即可得到
函数f (x)的单调递增区间.
解答:解:(1)∵ =(
=( cosx,0),
cosx,0), =(0,sinx)
=(0,sinx)
∴ +
+ =(
=( cosx,sinx),得(
cosx,sinx),得( +
+ )2=3cos2x+sin2x=1+2cos2x
)2=3cos2x+sin2x=1+2cos2x
f(x)=( +
+ )2十
)2十 sin2x=1+2cos2x+
sin2x=1+2cos2x+ sin2x
sin2x
=cos2x+ sin2x+2=2sin(2x+
sin2x+2=2sin(2x+ )+2
)+2
∴当2x+ =-
=- +2kπ(k∈Z),即x=-
+2kπ(k∈Z),即x=- +kπ(k∈Z)时,f(x)有最小值为0;
+kπ(k∈Z)时,f(x)有最小值为0;
(2)令- +2kπ≤2x+
+2kπ≤2x+ ≤
≤ +2kπ(k∈Z),
+2kπ(k∈Z),
得- +kπ≤x≤
+kπ≤x≤ +kπ(k∈Z)
+kπ(k∈Z)
∴函数f (x)的单调递增区间为[- +kπ,
+kπ, +kπ],其中k∈Z.
+kπ],其中k∈Z.
点评:本题以向量为载体,求三角函数的最值并讨论单调区间,着重考查了平面向量的坐标运算、三角恒等变换和三角函数的图象与性质等知识,属于中档题.
 +
+ )2=1+2cos2x,再结合二倍角的余弦公式和辅助角公式化简,得到f(x)=2sin(2x+
)2=1+2cos2x,再结合二倍角的余弦公式和辅助角公式化简,得到f(x)=2sin(2x+ )+2,最后根据正弦函数最值的结论,可得f(x)的最小值及取最小值时x的集合;
)+2,最后根据正弦函数最值的结论,可得f(x)的最小值及取最小值时x的集合;(2)根据(1)化简得的表达式,列出不等式-
 +2kπ≤2x+
+2kπ≤2x+ ≤
≤ +2kπ(k∈Z),解此不等式再将它变成区间,即可得到
+2kπ(k∈Z),解此不等式再将它变成区间,即可得到函数f (x)的单调递增区间.
解答:解:(1)∵
 =(
=( cosx,0),
cosx,0), =(0,sinx)
=(0,sinx)∴
 +
+ =(
=( cosx,sinx),得(
cosx,sinx),得( +
+ )2=3cos2x+sin2x=1+2cos2x
)2=3cos2x+sin2x=1+2cos2xf(x)=(
 +
+ )2十
)2十 sin2x=1+2cos2x+
sin2x=1+2cos2x+ sin2x
sin2x=cos2x+
 sin2x+2=2sin(2x+
sin2x+2=2sin(2x+ )+2
)+2∴当2x+
 =-
=- +2kπ(k∈Z),即x=-
+2kπ(k∈Z),即x=- +kπ(k∈Z)时,f(x)有最小值为0;
+kπ(k∈Z)时,f(x)有最小值为0;(2)令-
 +2kπ≤2x+
+2kπ≤2x+ ≤
≤ +2kπ(k∈Z),
+2kπ(k∈Z),得-
 +kπ≤x≤
+kπ≤x≤ +kπ(k∈Z)
+kπ(k∈Z)∴函数f (x)的单调递增区间为[-
 +kπ,
+kπ, +kπ],其中k∈Z.
+kπ],其中k∈Z.点评:本题以向量为载体,求三角函数的最值并讨论单调区间,着重考查了平面向量的坐标运算、三角恒等变换和三角函数的图象与性质等知识,属于中档题.

练习册系列答案
相关题目