题目内容
直线l:y=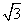 (x-2)和双曲线C:
(x-2)和双曲线C: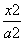 -
-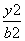 =1(a>0,b>0)交于A,B两点,且|AB|=
=1(a>0,b>0)交于A,B两点,且|AB|=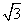 ,又l关于直线l1:y=
,又l关于直线l1:y= x对称的直线l2与x轴平行.
x对称的直线l2与x轴平行.
(1)求双曲线C的离心率;
(2)求双曲线C的方程.
解
(1)设双曲线C: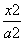 -
-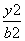 =1过一、三象限的渐近线l1:
=1过一、三象限的渐近线l1: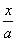 -
-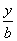 =0的倾斜角为α.
=0的倾斜角为α.
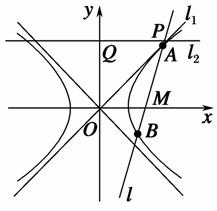
因为l和l2关于l1对称,记它们的交点为P.
而l2与x轴平行,记l2与y轴的交点为Q.
依题意有∠QPO=∠POM=∠OPM=α.
又l:y=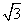 (x-2)的倾斜角为60°,则2α=60°,α=30°.
(x-2)的倾斜角为60°,则2α=60°,α=30°.
所以tan30°= =
=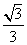 .
.
于是e2=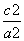 =1+
=1+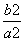 =1+
=1+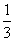 =
=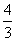 .所以e=
.所以e=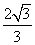 .
.
(2)由 =
=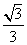 ,可设双曲线方程为
,可设双曲线方程为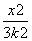 -
-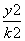 =1,即x2-3y2=3k2.
=1,即x2-3y2=3k2.
将y=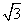 (x-2)代入x2-3y2=3k2,
(x-2)代入x2-3y2=3k2,
得x2-3·3(x-2)2=3k2.
化简得8x2-36x+36+3k2=0,则x1+x2=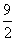 ,x1x2=
,x1x2=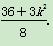 .
.
设A(x1,y1),B(x2,y2),
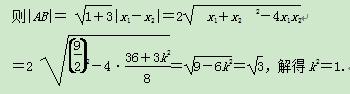 故所求双曲线C的方程为
故所求双曲线C的方程为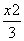 -y2=1.
-y2=1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
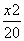 +
+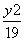 =1 B.
=1 B.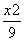 +
+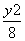 =1
=1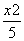 +
+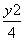 =1 D.
=1 D.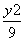 +
+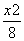 =1
=1 -
-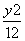 =1 B.
=1 B.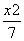 -
-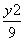 =1
=1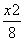 -
-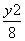 =1 D.
=1 D.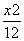 -
-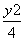 =1
=1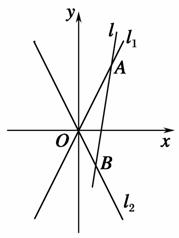
 ,则P点的轨迹方程是__________.
,则P点的轨迹方程是__________.