题目内容
已知双曲线E: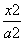 -
-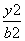 =1(a>0,b>0)的两条渐近线分别为l1:y=2x,l2:y=-2x.
=1(a>0,b>0)的两条渐近线分别为l1:y=2x,l2:y=-2x.
(1)求双曲线E的离心率.
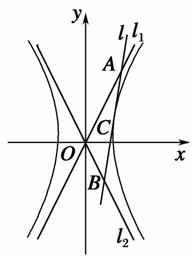
(2)如图,O为坐标原点,动直线l分别交直线l1,l2于A,B两点(A,B分别在第一、四象限),且△OAB的面积恒为8.试探究:是否存在总与直线l有且只有一个公共点的双曲线E?若存在,求出双曲线E的方程;若不存在,说明理由.
解 (1)因为双曲线E的渐近线分别为y=2x,y=-2x,
所以 =2,所以
=2,所以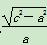 =2,故c=
=2,故c=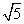 a,
a,
从而双曲线E的离心率e=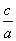 =
=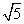 .
.
(2)由(1)知,双曲线E的方程为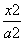 -
-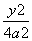 =1.
=1.
设直线l与x轴相交于点C.
当l⊥x轴时,若直线l与双曲线E有且只有一个公共点,
则|OC|=a,|AB|=4a.
又因为△OAB的面积为8,
所以 |OC|·|AB|=8,
|OC|·|AB|=8,
因此 a·4a=8,解得a=2,
a·4a=8,解得a=2,
此时双曲线E的方程为 -
-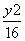 =1.
=1.
若存在满足条件的双曲线E,
则E的方程只能为 -
-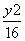 =1.
=1.
以下证明:当直线l不与x轴垂直时,双曲线E: -
-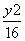 =1也满足条件.
=1也满足条件.
设直线l的方程为y=kx+m,依题意,得k>2或k<-2,则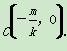 记A(x1,y1),B(x2,y2).
记A(x1,y1),B(x2,y2).
由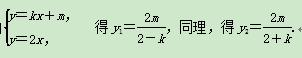
由S△OAB= |OC|·|y1-y2|,得
|OC|·|y1-y2|,得
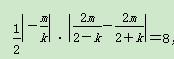 即m2=4|4-k2|=4(k2-4).
即m2=4|4-k2|=4(k2-4).
由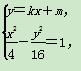 得(4-k2)x2-2kmx-m2-16=0.
得(4-k2)x2-2kmx-m2-16=0.
因为4-k2<0,
所以Δ=4k2m2+4(4-k2)(m2+16)
=-16(4k2-m2-16).
又因为m2=4(k2-4),
所以Δ=0,即l与双曲线E有且只有一个公共点.
因此,存在总与l有且只有一个公共点的双曲线E,且E的方程为 -
-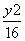 =1.
=1.

练习册系列答案
相关题目
 +y2=1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是( )
+y2=1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是( ) B.6
B.6 ,则C的方程是( )
,则C的方程是( ) =1 B.
=1 B. =1
=1 -
-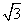 (x-2)和双曲线C:
(x-2)和双曲线C: 则|QF|=( )
则|QF|=( ) B.3
B.3 D.2
D.2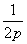 x2(p>0)的焦点与双曲线C2:
x2(p>0)的焦点与双曲线C2: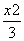 -y2=1的右焦点的连线交C1于第一象限的点M,若C1在点M处的切线平行于C2的一条渐近线,则p=( )
-y2=1的右焦点的连线交C1于第一象限的点M,若C1在点M处的切线平行于C2的一条渐近线,则p=( )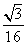 B.
B.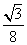
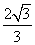 D.
D.
 (a>0),且满足条件sinC-sinB=
(a>0),且满足条件sinC-sinB= sinA,则动点A的轨迹方程是________.
sinA,则动点A的轨迹方程是________.