题目内容
(I)求函数
的单调区间；
(Ⅱ)函数在区间[1，2]上是否有零点，若有，求出零点，若没有，请说明理由；
(Ⅲ)若任意的
∈(1，2)且
≠
，证明：
(注：
解：
.
（Ⅰ） 
. ……………2分
，
，
在区间
和
上，
；在区间
上
，
故
的单调递增区间是和，单调递减区间是. …………4分
（Ⅱ）先求
在
的最大值.
由（Ⅰ）可知，
当
时，在
上单调递增，在
上单调递减，
故
.………………6分
由
可知
，
，
，
所以，
，
，
故不存在符合条件的
，使得
. ………………8分
（Ⅲ）当时，在上单调递增，在上单调递减，
只需证明
，
都成立，
也可得证命题成立．………………10分
设
，
，
在
上是减函数，
设
，
在上是增函数，
综上述命题成立. ………………12分
另解:
当
时，
，
在
上单调递减，在
上单调递增，
， 
，
，
，
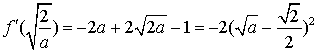
.………10分
由导数的几何意义有
对任意
，
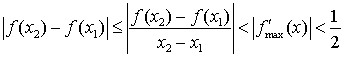．…………12分
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目