题目内容
(2013•天河区三模)已知函数f(x)=
sinxcosx-
cos2x,x∈R
(I) 求函数f(x)的最小正周期及单调增区间;
(Ⅱ)在△ABC中,角A、B、C所对的边分别是a、b、c,又f(
+
)=
,b=2,△ABC的面积等于3,求边长a的值.
| 3 |
| 1 |
| 2 |
(I) 求函数f(x)的最小正周期及单调增区间;
(Ⅱ)在△ABC中,角A、B、C所对的边分别是a、b、c,又f(
| A |
| 2 |
| π |
| 3 |
| 4 |
| 5 |
分析:(I) 函数f(x)的解析式利用二倍角的正弦、余弦函数公式化简,再利用两角和与差的正弦函数公式化为一个角的正弦函数,找出ω的值,即可求出函数的最小正周期,根据正弦函数的单调递增区间即可得到函数的单调增区间;
(Ⅱ)由f(
+
)=
,A∈(0,π),得到cosA与sinA的值,再利用三角形的面积公式及已知面积与b、sinA的值,求出c的值,再利用余弦定理即可求出a的值.
(Ⅱ)由f(
| A |
| 2 |
| π |
| 3 |
| 4 |
| 5 |
解答:解:(1)f(x)=
sin2x-
cos2x=sin(2x-
),
∵ω=2,
∴f(x)的最小正周期为π;
∵2kπ-
≤2x-
≤2kπ+
,k∈Z,
即kπ-
≤x≤kπ+
,k∈Z,
则函数的增区间为[kπ-
,kπ+
],k∈Z;
(2)∵f(
+
)=
,A∈(0,π),
∴cosA=
,sinA=
,
∵S=
bcsinA=3,b=2,sinA=
,
∴c=5,
由余弦定理a2=b2+c2-2bccosA=4+25-2×2×5×
=13,
∴a=
.
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
∵ω=2,
∴f(x)的最小正周期为π;
∵2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
即kπ-
| π |
| 6 |
| π |
| 3 |
则函数的增区间为[kπ-
| π |
| 6 |
| π |
| 3 |
(2)∵f(
| A |
| 2 |
| π |
| 3 |
| 4 |
| 5 |
∴cosA=
| 4 |
| 5 |
| 3 |
| 5 |
∵S=
| 1 |
| 2 |
| 3 |
| 5 |
∴c=5,
由余弦定理a2=b2+c2-2bccosA=4+25-2×2×5×
| 4 |
| 5 |
∴a=
| 13 |
点评:此题考查了两角和与差的正弦函数公式,余弦定理,三角形的面积公式,正弦函数的单调性,以及三角函数的周期性及其求法,熟练掌握公式及定理是解本题的关键.

练习册系列答案
相关题目
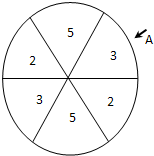 (2013•天河区三模)如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(a,b)(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).
(2013•天河区三模)如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(a,b)(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).