题目内容
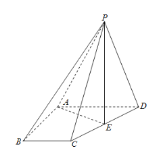
【题目】（文科）已知四棱锥
的底面ABCD为直角梯形，
，
，
，
为正三角形.
（1）点M为棱AB上一点，若
平面SDM，
，求实数λ的值；
（2）若
，求四棱锥的体积.
【答案】（1）
；（2）.
【解析】
（1）由线面平行的性质定理得
，从而知
是
中点，
可求；
（2）由已知证得所以
平面SCD，即得平面
平面ABCD.，因此在平面SCD内过点S作SE垂直CD交CD的延长线于点E，就有
平面ABCD，这就是棱锥的高．由
，得
，再由
，
，得
，从而有
，于是棱锥体积可求．
（1）若
平面SDM，
平面ABCD，平面
平面
，
所以，
因为
，所以四边形BCDM为平行四边形.
又因为
，
所以M为AB的中点.
因为
，
所以
.
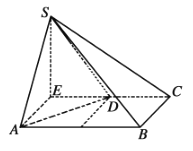
（2）因为，
，所以
，
又
，
，
所以平面SCD，
又平面ABCD
所以平面平面ABCD.
在平面SCD内过点S作SE垂直CD交CD的延长线于点E，
又平面
平面
，
所以平面ABCD，
连接AE，在
和
中，
因为，所以
，
由题易知，，
所以，
所以，
底面ABCD为直角梯形，，，
，
，
四棱锥的体积
.
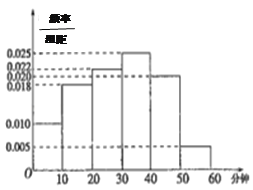
【题目】电视传媒公司为了解某地区电视观众对某类体育节目的收视情况，随机抽取了100名观众进行调查．下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图：
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”．
（1）根据已知条件完成上面的2×2列联表，若按95%的可靠性要求，并据此资料，你是否认为“体育迷”与性别有关？
（2）现在从该地区非体育迷的电视观众中，采用分层抽样方法选取5名观众，求从这5名观众选取两人进行访谈，被抽取的2名观众中至少有一名女生的概率．
附：
P（K2≥k） | 0.05 | 0.01 |
k | 3.841 | 6.635 |
【题目】高三学生为了迎接高考，要经常进行模拟考试，锻炼应试能力，某学生从升入高三到高考要参加10次模拟考试，下面是高三第一学期某学生参加5次模拟考试的数学成绩表：
模拟考试第x次 | 1 | 2 | 3 | 4 | 5 |
考试成绩y分 | 90 | 100 | 105 | 105 | 100 |
（1）已知该考生的模拟考试成绩y与模拟考试的次数x满足回归直线方程
，若高考看作第11次模拟考试，试估计该考生的高考数学成绩；
（2）把这5次模拟考试的数学成绩单放在5个相同的信封中，从中随机抽取3份试卷的成绩单进行研究，设抽取考试成绩不等于平均值
的个数为
，求出的分布列与数学期望.
参考公式：
.
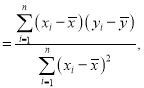
【题目】2019年10月18日-27日，第七届世界军人运动会在湖北武汉举办，中国代表团共获得133金64银42铜，共239枚奖牌.为了调查各国参赛人员对主办方的满意程度，研究人员随机抽取了500名参赛运动员进行调查，所得数据如下所示，现有如下说法：①在参与调查的500名运动员中任取1人，抽到对主办方表示满意的男性运动员的概率为
；②在犯错误的概率不超过1%的前提下可以认为“是否对主办方表示满意与运动员的性别有关”；③没有99.9%的把握认为“是否对主办方表示满意与运动员的性别有关”；则正确命题的个数为（ ）附：
男性运动员 | 女性运动员 | |||||
对主办方表示满意 | 200 | 220 | ||||
对主办方表示不满意 | 50 | 30 | ||||
| 0.100 | 0.050 | 0.010 | 0.001 | ||
k | 2.706 | 3.841 | 6.635 | 10.828 | ||
A.0B.1C.2D.3
