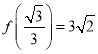题目内容
【题目】已知函数![]()
![]() 的周期为
的周期为![]() ,图象的一个对称中心为
,图象的一个对称中心为![]() .将函数
.将函数![]() 图象上所有点的横坐标伸长到原来的
图象上所有点的横坐标伸长到原来的![]() 倍(纵坐标不变),再将所得到的图象向右平移
倍(纵坐标不变),再将所得到的图象向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象.
的图象.
(1)求函数![]() 与
与![]() 的解析式;
的解析式;
(2)(理)求证:存在![]() ,使得
,使得![]() ,
,![]() ,
,![]() 能按照某种顺序成等差数列.
能按照某种顺序成等差数列.
(3)(文)定义:当函数取得最值时,函数图像上对应的点称为函数的最值点,如果函数![]() 的图像上至少有一个最大值点和一个最小值点在圆
的图像上至少有一个最大值点和一个最小值点在圆![]() 的内部或圆周上,求
的内部或圆周上,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() (2)证明见解析 (3)
(2)证明见解析 (3)![]()
【解析】
(1)先根据周期得![]() 再根据对称中心得
再根据对称中心得![]() ,最后根据图象变换规律得结果;
,最后根据图象变换规律得结果;
(2)先确定大小关系,再根据等差中项性质得方程,最后利用零点存在定理证明方程有解;
(3)先求函数最值点坐标,再确定与原点距离最近的最大值和最小值点坐标,代入解不等式得结果.
解:(1)、由函数![]() 的周期为
的周期为![]() ,
,![]() ,得
,得![]() ,
,
又曲线![]() 的一个对称中心为
的一个对称中心为![]() ,
,![]() ,
,
故![]() ,得
,得![]() ,所以
,所以![]()
将函数![]() 图象上所有点的横坐标伸长到原来的
图象上所有点的横坐标伸长到原来的![]() 倍(纵坐标不变)后可得
倍(纵坐标不变)后可得![]() 的图象,再将
的图象,再将![]() 的图象向右平移
的图象向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象,所以
的图象,所以![]()
(2)、(理)当![]() 时,
时,![]() ,
,![]() ,
,
所以![]()
问题转化为方程![]() 在
在![]() 内是否有解.
内是否有解.
设![]() ,
,![]()
![]()
![]() ,
,![]() ,
,
且函数![]() 的图象连续不断,故可知函数
的图象连续不断,故可知函数![]() 在
在![]() 内存在零点
内存在零点![]()
(3)(文)函数![]() 当
当![]() 时取得最大值或最小值,当
时取得最大值或最小值,当![]() ,即与原点距离最近的最大值和最小值点分别是点
,即与原点距离最近的最大值和最小值点分别是点![]() 和
和![]() ,于是有
,于是有![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]()

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案【题目】我市为改善空气环境质量,控制大气污染,政府相应出台了多项改善环境的措施.其中一项是为了减少燃油汽车对大气环境污染.从2018年起大力推广使用新能源汽车,鼓励市民如果需要购车,可优先考虑选用新能源汽车.政府对购买使用新能源汽车进行购物补贴,同时为了地方经济发展,对购买本市企业生产的新能源汽车比购买外地企业生产的新能源汽车补贴高.所以市民对购买使用本市企业生产的新能源汽车的满意度也相应有所提高.有关部门随机抽取本市本年度内购买新能源汽车的![]() 户,其中有
户,其中有![]() 户购买使用本市企业生产的新能源汽车,对购买使用新能源汽车的满意度进行调研,满意度以打分的形式进行.满分
户购买使用本市企业生产的新能源汽车,对购买使用新能源汽车的满意度进行调研,满意度以打分的形式进行.满分![]() 分,将分数按照
分,将分数按照![]() 分成5组,得如下频率分布直方图.
分成5组,得如下频率分布直方图.

(1)若本次随机抽取的样本数据中购买使用本市企业生产的新能源汽车的用户中有![]() 户满意度得分不少于
户满意度得分不少于![]() 分,把得分不少于
分,把得分不少于![]() 分为满意.根据提供的条件数据,完成下面的列联表.
分为满意.根据提供的条件数据,完成下面的列联表.
满意 | 不满意 | 总计 | |
购本市企业生产的新能源汽车户数 | |||
购外地企业生产的新能源汽车户数 | |||
总计 |
并判断是否有![]() 的把握认为购买使用新能源汽车的满意度与产地有关?
的把握认为购买使用新能源汽车的满意度与产地有关?
(2)以频率作为概率,政府对购买使用新能源汽车的补贴标准是:购买本市企业生产的每台补贴![]() 万元,购买外地企业生产的每台补贴
万元,购买外地企业生产的每台补贴![]() 万元.但本市本年度所有购买新能源汽车的补贴每台的期望值不超过
万元.但本市本年度所有购买新能源汽车的补贴每台的期望值不超过![]() 万元.则购买外地产的新能源汽车每台最多补贴多少万元?
万元.则购买外地产的新能源汽车每台最多补贴多少万元?
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|