题目内容
(Ⅰ)已知函数 ,若存在
,若存在 ,使得
,使得 ,则称
,则称 是函数
是函数 的一个不动点,设二次函数
的一个不动点,设二次函数 .
.
(Ⅰ) 当 时,求函数
时,求函数 的不动点;
的不动点;
(Ⅱ) 若对于任意实数 ,函数
,函数 恒有两个不同的不动点,求实数
恒有两个不同的不动点,求实数 的取值范围;
的取值范围;
(Ⅲ) 在(Ⅱ)的条件下,若函数 的图象上
的图象上 两点的横坐标是函数
两点的横坐标是函数 的不动点,且直线
的不动点,且直线 是线段
是线段 的垂直平分线,求实数
的垂直平分线,求实数 的取值范围.
的取值范围.
 ,若存在
,若存在 ,使得
,使得 ,则称
,则称 是函数
是函数 的一个不动点,设二次函数
的一个不动点,设二次函数 .
. (Ⅰ) 当
 时,求函数
时,求函数 的不动点;
的不动点;(Ⅱ) 若对于任意实数
 ,函数
,函数 恒有两个不同的不动点,求实数
恒有两个不同的不动点,求实数 的取值范围;
的取值范围;(Ⅲ) 在(Ⅱ)的条件下,若函数
 的图象上
的图象上 两点的横坐标是函数
两点的横坐标是函数 的不动点,且直线
的不动点,且直线 是线段
是线段 的垂直平分线,求实数
的垂直平分线,求实数 的取值范围.
的取值范围.(Ⅰ)函数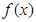 的不动点为
的不动点为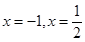 。
。
(Ⅱ)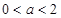
(Ⅲ)实数 的取值范围
的取值范围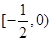 .
.
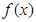 的不动点为
的不动点为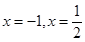 。
。(Ⅱ)
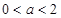
(Ⅲ)实数
 的取值范围
的取值范围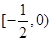 .
.试题分析:
思路分析:(Ⅰ) 解方程确定函数
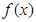 的不动点为
的不动点为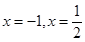 。
。(Ⅱ)由题意,得到方程
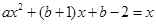 恒有两个不相等的实数根,
恒有两个不相等的实数根,根据判别式
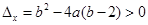 ,解得
,解得 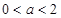 。
。(Ⅲ)设函数
 的两个不同的不动点为
的两个不同的不动点为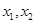 得到
得到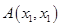 ,
,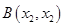 ,
,且
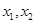 是
是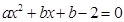 的两个不等实根, 得到
的两个不等实根, 得到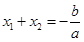
直至
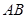 中点坐标为
中点坐标为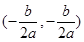 。根据
。根据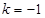 ,且
,且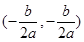 在直线
在直线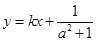 上得到a,b的关系。
上得到a,b的关系。解:(Ⅰ) 当
 时,
时,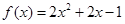 ,
,解
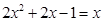 ,得
,得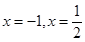 。
。所以函数
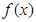 的不动点为
的不动点为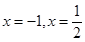 。
。(Ⅱ)因为 对于任意实数
 ,函数
,函数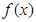 恒有两个不同的不动点,
恒有两个不同的不动点,所以,对于任意实数
 ,方程
,方程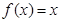 恒有两个不相等的实数根,
恒有两个不相等的实数根,即方程
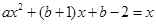 恒有两个不相等的实数根,
恒有两个不相等的实数根,所以
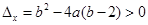 ,
,即 对于任意实数
 ,
,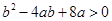 ,
,所以
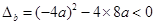 ,解得
,解得 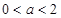
(Ⅲ)设函数
 的两个不同的不动点为
的两个不同的不动点为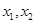 ,则
,则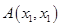 ,
,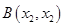
且
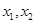 是
是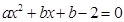 的两个不等实根, 所以
的两个不等实根, 所以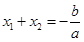
直线
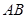 的斜率为1,线段
的斜率为1,线段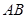 中点坐标为
中点坐标为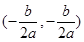
因为 直线
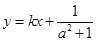 是线段
是线段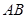 的垂直平分线,
的垂直平分线,所以
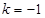 ,且
,且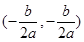 在直线
在直线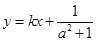 上
上则
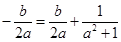

所以
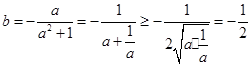 当且仅当
当且仅当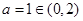 时等号成立
时等号成立又
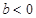 所以 实数
所以 实数 的取值范围
的取值范围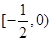 .
.点评:难题,本题给出“不动点”的概念,解题过程中,应注意理解并应用这一概念。将问题转化成一元二次方程问题,结合直线方程,应用均值定理,达到解题目的。

练习册系列答案
相关题目
 ,其中a是实数.设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的两点,且x1<x2.
,其中a是实数.设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的两点,且x1<x2.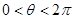 ,且方程
,且方程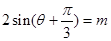 有两个不同的实数根,则这两个实根的和为 .
有两个不同的实数根,则这两个实根的和为 .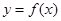 对任意的
对任意的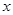 都满足
都满足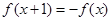 ,当
,当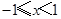 时,
时,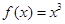 ,若函数
,若函数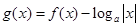 至少6个零点,则
至少6个零点,则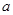 取值范围是( )
取值范围是( )
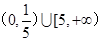
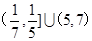
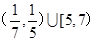
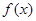 的图象恰好通过
的图象恰好通过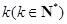 个格点,则称函数
个格点,则称函数 阶格点函数. 给出下列4个函数:
阶格点函数. 给出下列4个函数: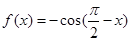 ;②
;②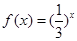 ;③
;③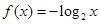 ;④
;④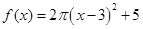 .
. 年(
年(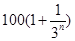 万元.设从2012年起的前
万元.设从2012年起的前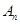 万元,开发新项目的累计利润为
万元,开发新项目的累计利润为 万元(须扣除开发所投入资金).
万元(须扣除开发所投入资金).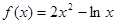 在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围是( )
在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围是( )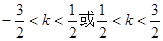
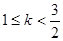
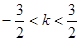

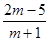 ,则实数m的取值集合是( )
,则实数m的取值集合是( )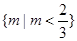
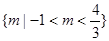
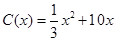 上的函数
上的函数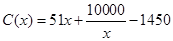 满足
满足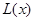 .若当
.若当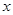 时.
时.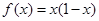 ,则当
,则当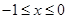 时,
时,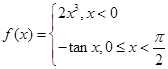 = .
= .