题目内容
如图,是某四棱锥的三视图,则该几何体的表面积为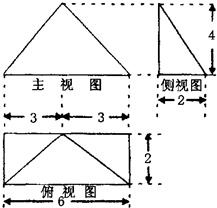
分析:几何体是一个四棱锥,四棱锥的底面是一个长为6,宽为2的矩形,顶点底面的面积,四棱锥的一个侧面与底面垂直,四棱锥的高是4,根据勾股定理做出三角形的高,做出4个三角形的面积,求和得到结果.
解答:解:由三视图知,几何体是一个四棱锥,
∵四棱锥的底面是一个长为6,宽为2的矩形,
∴面积是6×2=12,
∵四棱锥的一个侧面与底面垂直,
顶点在底面上的射影是垂直于底面的这条棱与底面的交线的中点,
四棱锥的高是4,
和垂直于底面的侧面相对的面的高是
=2
,
∴四个侧面的面积是
×6×2
+
×6×4+2×
×2×5=34+6
,
故答案为:34+6
∵四棱锥的底面是一个长为6,宽为2的矩形,
∴面积是6×2=12,
∵四棱锥的一个侧面与底面垂直,
顶点在底面上的射影是垂直于底面的这条棱与底面的交线的中点,
四棱锥的高是4,
和垂直于底面的侧面相对的面的高是
| 22+42 |
| 5 |
∴四个侧面的面积是
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
故答案为:34+6
| 5 |
点评:本题考查由三视图求几何体的表面积,考查由三视图还原几何体,并且顶点几何体各个部分的长度,本题考查利用勾股定理求三角形的高,本题是一个基础题.

练习册系列答案
相关题目
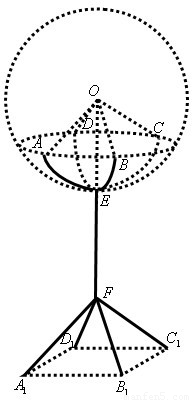
 (2013•江苏一模)某部门要设计一种如图所示的灯架,用来安装球心为O,半径为R(米)的球形灯泡.该灯架由灯托、灯杆、灯脚三个部件组成,其中圆弧形灯托
(2013•江苏一模)某部门要设计一种如图所示的灯架,用来安装球心为O,半径为R(米)的球形灯泡.该灯架由灯托、灯杆、灯脚三个部件组成,其中圆弧形灯托
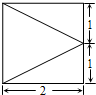 已知某四棱锥,底面是边长为2的正方形,且俯视图如图所示.
已知某四棱锥,底面是边长为2的正方形,且俯视图如图所示.

 ,
, ,
, ,
,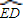 所在圆的圆心都是O、半径都是R(米)、圆弧的圆心角都是θ(弧度);灯杆EF垂直于地面,杆顶E到地面的距离为h(米),且h>R;灯脚FA1,FB1,FC1,FD1是正四棱锥F-A1B1C1D1的四条侧棱,正方形A1B1C1D1的外接圆半径为R(米),四条灯脚与灯杆所在直线的夹角都为θ(弧度).已知灯杆、灯脚的造价都是每米a(元),灯托造价是每米
所在圆的圆心都是O、半径都是R(米)、圆弧的圆心角都是θ(弧度);灯杆EF垂直于地面,杆顶E到地面的距离为h(米),且h>R;灯脚FA1,FB1,FC1,FD1是正四棱锥F-A1B1C1D1的四条侧棱,正方形A1B1C1D1的外接圆半径为R(米),四条灯脚与灯杆所在直线的夹角都为θ(弧度).已知灯杆、灯脚的造价都是每米a(元),灯托造价是每米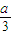 (元),其中R,h,a都为常数.设该灯架的总造价为y(元).
(元),其中R,h,a都为常数.设该灯架的总造价为y(元).