题目内容
（2013•江苏一模）某部门要设计一种如图所示的灯架，用来安装球心为O，半径为R（米）的球形灯泡．该灯架由灯托、灯杆、灯脚三个部件组成，其中圆弧形灯托 |
| EA |
|
| EB |
|
| EC |
|
| ED |
| a |
| 3 |
（1）求y关于θ的函数关系式；
（2）当θ取何值时，y取得最小值？
分析：（1）由题意把4根灯脚及灯架写成是关于θ的表达式，运用弧长公式把4根灯托也用θ表示，然后乘以各自的造价作和即可得到y关于θ的函数关系式；
（2）对（1）求出的函数式进行求导计算，分析得到当θ=
时函数取得极小值，也就是最小值．
（2）对（1）求出的函数式进行求导计算，分析得到当θ=
| π |
| 3 |
解答：解：如图，
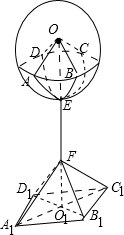
（1）延长EF与地面交于O1，由题意知：∠A1FO1=θ，且FO1=
，
从而EF=h-
，A1F=
，
则y=4θ•R•
+(h-
+
)a，(θ∈(0，
))．
（2）y=Ra(
+
)+ha，
设f(θ)=
+
，
令f′(θ)=
+
=
=
=0．
得：1-2cosθ=0，所以θ=
．
当θ∈(0，
)时，f′（θ）＜0．
当θ∈(
，
)时，f′（θ）＞0．
设θ∈(θ0，
)，其中tanθ0=
＜1，∴θ0＜
．
∴
∈(θ0，
)，∴θ=
时，y最小．
答：当θ=
时，灯架造价取得最小值．
（1）延长EF与地面交于O1，由题意知：∠A1FO1=θ，且FO1=
| R |
| tanθ |
从而EF=h-
| R |
| tanθ |
| R |
| sinθ |
则y=4θ•R•
| a |
| 3 |
| R |
| tanθ |
| 4R |
| sinθ |
| π |
| 2 |
（2）y=Ra(
| 4θ |
| 3 |
| 4-cosθ |
| sinθ |
设f(θ)=
| 4θ |
| 3 |
| 4-cosθ |
| sinθ |
令f′(θ)=
| 4 |
| 3 |
| sin2θ-cosθ(4-cosθ) |
| sin2θ |
| 4sin2θ+3-12cosθ |
| 3sin2θ |
=
| (1-2cosθ)(7+2cosθ) |
| 3sin2θ |
得：1-2cosθ=0，所以θ=
| π |
| 3 |
当θ∈(0，
| π |
| 3 |
当θ∈(
| π |
| 3 |
| π |
| 2 |
设θ∈(θ0，
| π |
| 2 |
| R |
| h |
| π |
| 4 |
∴
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
答：当θ=
| π |
| 3 |
点评：本题考查了函数模型的选择及应用，考查了利用导数求函数的最值，解答此题时要注意实际问题要注明符合实际意义的定义域，此题是中档题．
练习册系列答案
阅读快车系列答案
相关题目