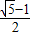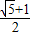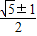Question

直角三角形三边成等比数列，公比为q，则q²的值为（　　）

• A．2
• B．

  5 -1

  2

• C．

  5 +1

  2

• D．

  5 ±1

  2

Answer 1

分析：由直角三角形的三边成等比数列，公比为q，设三角形三边分别为a，aq，aq²，根据勾股定理列出关系式，根据a大于0，化简可得关于q的方程，求出方程的解即可得到q的值．

解答：解：设直角三角形较短的直角边为a（a＞0），则其它两边分别为aq，aq²，
根据勾股定理得：a²+（aq）²=（aq²）²，
整理得：q⁴-q²-1=0，
解得：q²=

1+ 5

2

或q²=

1- 5

2

（舍去），
则q²的值为

1+ 5

2

．
故选C

点评：此题考查了等比数列的性质，勾股定理，以及一元二次方程的解法，熟练掌握等比数列的性质是解本题的关键．