题目内容
已知函数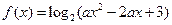
(1)当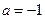 时,求该函数的定义域和值域;
时,求该函数的定义域和值域;
(2)如果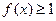 在区间
在区间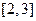 上恒成立,求实数
上恒成立,求实数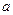 的取值范围.
的取值范围.
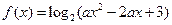
(1)当
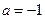 时,求该函数的定义域和值域;
时,求该函数的定义域和值域;(2)如果
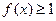 在区间
在区间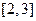 上恒成立,求实数
上恒成立,求实数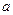 的取值范围.
的取值范围.(1)定义域为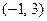 ;值域为
;值域为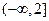 (2)
(2)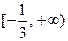
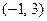 ;值域为
;值域为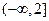 (2)
(2)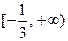
(1) 当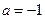 时,
时,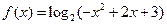
令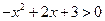 ,解得
,解得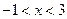
所以函数 的定义域为
的定义域为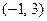 .
.
令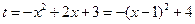 ,则
,则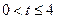
所以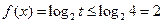
因此函数 的值域为
的值域为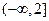
(2) 解法一: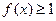 在区间
在区间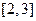 上恒成立等价于
上恒成立等价于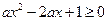 在区间
在区间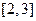 上恒成立
上恒成立
令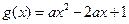
当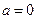 时,
时,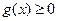 ,所以
,所以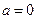 满足题意.
满足题意.
当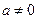 时,
时,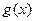 是二次函数,对称轴为
是二次函数,对称轴为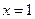 ,
,
当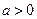 时,函数
时,函数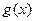 在区间
在区间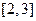 上是增函数,
上是增函数,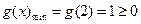 ,所以
,所以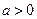 满足题意;
满足题意;
当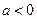 时,函数
时,函数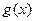 在区间
在区间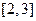 上是减函数,
上是减函数,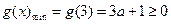 ,
,
解得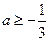 ,所以
,所以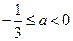 满足题意.
满足题意.
综上,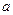 的取值范围是
的取值范围是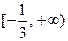
解法二: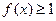 在区间
在区间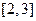 上恒成立等价于
上恒成立等价于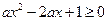 在区间
在区间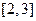 上恒成立
上恒成立
由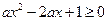 且
且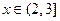 时,
时,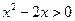 ,得
,得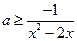
因为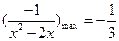 ,所以
,所以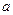 的取值范围是
的取值范围是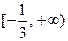 .
.
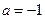 时,
时,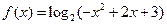
令
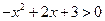 ,解得
,解得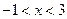
所以函数
 的定义域为
的定义域为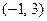 .
.令
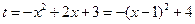 ,则
,则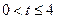
所以
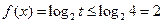
因此函数
 的值域为
的值域为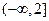
(2) 解法一:
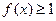 在区间
在区间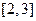 上恒成立等价于
上恒成立等价于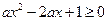 在区间
在区间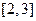 上恒成立
上恒成立令
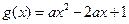
当
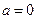 时,
时,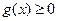 ,所以
,所以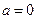 满足题意.
满足题意.当
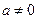 时,
时,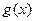 是二次函数,对称轴为
是二次函数,对称轴为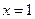 ,
,当
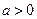 时,函数
时,函数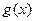 在区间
在区间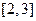 上是增函数,
上是增函数,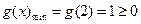 ,所以
,所以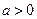 满足题意;
满足题意;当
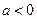 时,函数
时,函数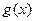 在区间
在区间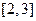 上是减函数,
上是减函数,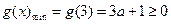 ,
,解得
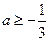 ,所以
,所以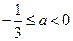 满足题意.
满足题意.综上,
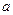 的取值范围是
的取值范围是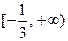
解法二:
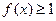 在区间
在区间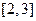 上恒成立等价于
上恒成立等价于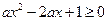 在区间
在区间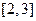 上恒成立
上恒成立由
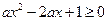 且
且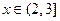 时,
时,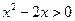 ,得
,得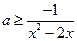
因为
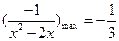 ,所以
,所以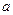 的取值范围是
的取值范围是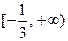 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
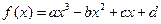 (a,b,c,d为实常数)的图象关于原点对称,且当x=1时f(x)取得极值
(a,b,c,d为实常数)的图象关于原点对称,且当x=1时f(x)取得极值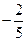 .
.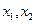 ∈[-1,1],不等式
∈[-1,1],不等式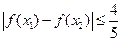 成立;
成立;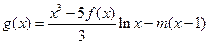 在区间(1,∞)内无零点,求实数m的取值范围.
在区间(1,∞)内无零点,求实数m的取值范围.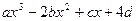 ( a , b , c , d∈R )的图象关于原点对称,且x = 1时,f(x)取极小值
( a , b , c , d∈R )的图象关于原点对称,且x = 1时,f(x)取极小值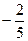 。
。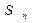 ∈[-1,1]时,求证:| f (
∈[-1,1]时,求证:| f (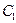 )-f(
)-f( )|≤
)|≤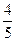 。
。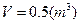 为定值时,它的表面和三层隔板(包括冷冻室的底层)面积之和S值最小
为定值时,它的表面和三层隔板(包括冷冻室的底层)面积之和S值最小 (参考数据:
(参考数据: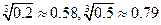 ,
,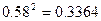 ,
,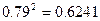 )
)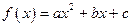 .
. 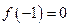 ,试判断函数
,试判断函数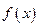 零点个数;
零点个数;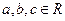 ,使
,使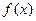 同时满足以下条件①对
同时满足以下条件①对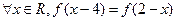 ,且
,且 ;②对
;②对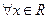 ,都有
,都有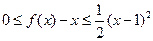 。若存在,求出
。若存在,求出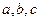 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。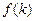 是满足不等式
是满足不等式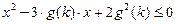 的自然数
的自然数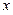 的个数,其中
的个数,其中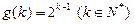 .
.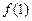 的值;
的值; ,令
,令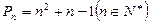 ,试比较
,试比较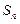 与
与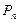 的大小.
的大小. ,例如:1
,例如:1 2=1,3
2=1,3 的值域为 .
的值域为 .  +lnx的图像在点P(m,f(m))处的切线方程为y="x" ,
+lnx的图像在点P(m,f(m))处的切线方程为y="x" ,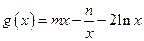 .
.  恒成立;
恒成立;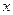 的方程:
的方程: 根的个数.
根的个数.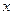 表示床价,用
表示床价,用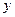 表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入)
表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入)