题目内容
已知一元二次方程:(1)mx2-4x+4=0;(2)x2-4mx+4m2-4m-5=0(m∈Z),求方程(1)和(2)的根都是整数的充要条件.
解:方程(1)有实根?△1=16-16m≥0,即m≤1;
方程(2)有实根?△2=16m2- ,
,
由 .
.
当m=-1时,方程(1)为x2+4x-4=0,无整数解;
当m=0 时,方程(2)为x2=5,无整数解;
当m=1时,方程(1)有整数解x=2,方程(2)有整数解x=-1或5,
从而(1)、(2)都有整数解?m=1.
反过来,由m=1,可推得方程(1)、(2)都有整数解,
所以方程(1)、(2)都有整数解的充要条件是m=1.
分析:先通过二次方程的判别式判断出两个方程有实根的m的范围,求出整数m的值,将各个m的值代入两个方程,判断出有整数根的m的值,反之判断出两个方程都有实根.
点评:本题考查二次方程有实根的条件及求一个命题充要条件的方法:一般先求出必要条件在证明充分性.
方程(2)有实根?△2=16m2-
 ,
,由
 .
.当m=-1时,方程(1)为x2+4x-4=0,无整数解;
当m=0 时,方程(2)为x2=5,无整数解;
当m=1时,方程(1)有整数解x=2,方程(2)有整数解x=-1或5,
从而(1)、(2)都有整数解?m=1.
反过来,由m=1,可推得方程(1)、(2)都有整数解,
所以方程(1)、(2)都有整数解的充要条件是m=1.
分析:先通过二次方程的判别式判断出两个方程有实根的m的范围,求出整数m的值,将各个m的值代入两个方程,判断出有整数根的m的值,反之判断出两个方程都有实根.
点评:本题考查二次方程有实根的条件及求一个命题充要条件的方法:一般先求出必要条件在证明充分性.

练习册系列答案
相关题目
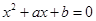 的一个根在-2与-1之间,另一个根在1与2之间,试求点
的一个根在-2与-1之间,另一个根在1与2之间,试求点 的轨迹及
的轨迹及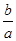 的范围.
的范围.