题目内容
已知函数f(x)=tgx,x∈(0,| π |
| 2 |
| π |
| 2 |
证明
| 1 |
| 2 |
| x1+x2 |
| 2 |
分析:欲证不等式的左边是
(tgx1+tgx2),将正切化成正余弦,通分后利用三角函数的和角公式和积化和差公式,结合三角函数的有界性进行放缩,最后利用半角公式即可证得.
| 1 |
| 2 |
解答:证明:tgx1+tgx2=
+
=
=
=
∵x1,x2∈(0,
),x1≠x2,
∴2sin(x1+x2)>0,cosx1cosx2>0,且0<cos(x1-x2)<1,
从而有0<cos(x1+x2)+cos(x1-x2)<1+cos(x1+x2),
由此得tgx1+tgx2>=
,∴
(tgx1+tgx2)>tg
,
即
[f(x1)+f(x2)]>f(
).
| sinx1 |
| cosx1 |
| sinx2 |
| cosx2 |
| sinx1cosx2+cosx1sinx2 |
| cosx1cosx2 |
=
| sin(x1+x2) |
| cosx1cosx2 |
| 2sin(x1+x2) |
| cos(x1+x2)+cos(x1-x2) |
∵x1,x2∈(0,
| π |
| 2 |
∴2sin(x1+x2)>0,cosx1cosx2>0,且0<cos(x1-x2)<1,
从而有0<cos(x1+x2)+cos(x1-x2)<1+cos(x1+x2),
由此得tgx1+tgx2>=
| 2sin(x1+x2) |
| 1+cos(x1+x2) |
| 1 |
| 2 |
| x1+x2 |
| 2 |
即
| 1 |
| 2 |
| x1+x2 |
| 2 |
点评:本小题考查三角函数基础知识、三角函数性质及推理能力.

练习册系列答案
相关题目
 -1)+lnx,t为常数,且t>0.
-1)+lnx,t为常数,且t>0.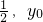 )处的切线方程为2x+y-2+ln2,求t和y0的值;
)处的切线方程为2x+y-2+ln2,求t和y0的值; -1)+lnx,t为常数,且t>0.
-1)+lnx,t为常数,且t>0. )处的切线方程为2x+y-2+ln2,求t和y的值;
)处的切线方程为2x+y-2+ln2,求t和y的值;