题目内容
已知函数f(x)=t( -1)+lnx,t为常数,且t>0.
-1)+lnx,t为常数,且t>0.(1)若曲线y=f(x)上一点(
 )处的切线方程为2x+y-2+ln2,求t和y的值;
)处的切线方程为2x+y-2+ln2,求t和y的值;(2)若f(x)在区间[1,+∞)上是单调递增函数,求t的取值范围.
【答案】分析:(1)首先求出函数的导数,然后根据条件列方程组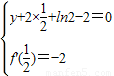 并解方程组即可求出结果;
并解方程组即可求出结果;
(2)由f(x)在区间[1,+∞)上是单调递增函数⇒f'(x)≥0在x∈[1,+∝)上恒成立,然后分离参数t≤x恒成立,进而根据x≥1,求出t的范围.
解答:解:(1)∵f(x)=t(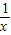 -1)+lnx
-1)+lnx
∴f'(x)=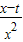
由题意知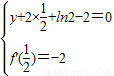
解得:
(2)若f(x)在区间[1,+∞)上是单调递增函数
则f'(x)≥0在x∈[1,+∝)上恒成立,即t≤x恒成立
∵x≥1
∴t≤1
又∵t>0
∴0<t≤1
点评:本题考查了利用导数研究函数的单调性以及求切线方程,(2)问中将问题转化成f'(x)≥0在x∈[1,+∝)上恒成立,是解题的关键,属于中档题.
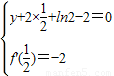 并解方程组即可求出结果;
并解方程组即可求出结果;(2)由f(x)在区间[1,+∞)上是单调递增函数⇒f'(x)≥0在x∈[1,+∝)上恒成立,然后分离参数t≤x恒成立,进而根据x≥1,求出t的范围.
解答:解:(1)∵f(x)=t(
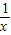 -1)+lnx
-1)+lnx∴f'(x)=
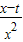
由题意知
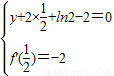
解得:

(2)若f(x)在区间[1,+∞)上是单调递增函数
则f'(x)≥0在x∈[1,+∝)上恒成立,即t≤x恒成立
∵x≥1
∴t≤1
又∵t>0
∴0<t≤1
点评:本题考查了利用导数研究函数的单调性以及求切线方程,(2)问中将问题转化成f'(x)≥0在x∈[1,+∝)上恒成立,是解题的关键,属于中档题.

练习册系列答案
相关题目
 -1)+lnx,t为常数,且t>0.
-1)+lnx,t为常数,且t>0.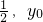 )处的切线方程为2x+y-2+ln2,求t和y0的值;
)处的切线方程为2x+y-2+ln2,求t和y0的值;