题目内容
已知圆O: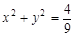 ,直线l:
,直线l: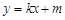 与椭圆C:
与椭圆C: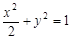 相交于P、Q两点,O为原点.
相交于P、Q两点,O为原点.
(Ⅰ)若直线l过椭圆C的左焦点,且与圆O交于A、B两点,且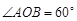 ,求直线l的方程;
,求直线l的方程;
(Ⅱ)如图,若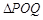 重心恰好在圆上,求m的取值范围.
重心恰好在圆上,求m的取值范围.
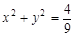 ,直线l:
,直线l: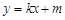 与椭圆C:
与椭圆C: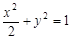 相交于P、Q两点,O为原点.
相交于P、Q两点,O为原点.(Ⅰ)若直线l过椭圆C的左焦点,且与圆O交于A、B两点,且
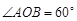 ,求直线l的方程;
,求直线l的方程;(Ⅱ)如图,若
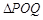 重心恰好在圆上,求m的取值范围.
重心恰好在圆上,求m的取值范围.
(1) (2)
(2) 或
或 .
.
 (2)
(2) 或
或 .
.试题分析:解(Ⅰ)左焦点坐标为
 ,设直线l的方程为
,设直线l的方程为 .
.由
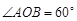 得,圆心O到直线l的距离
得,圆心O到直线l的距离 ,
,又
 ,∴
,∴ ,解得,
,解得, .∴ 直线l的方程为
.∴ 直线l的方程为 .
.(Ⅱ)设
 ,
, .
.由
 得
得 .
.由
 ,得
,得 …(※),且
…(※),且 .
.由
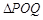 重心恰好在圆
重心恰好在圆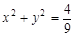 上,得
上,得 ,
,即
 ,即
,即 .
.∴
 ,化简得
,化简得 ,代入(※)得
,代入(※)得 .
.又
 .
.由
 , 得
, 得 ,∴
,∴ ,
,∴
 ,得m的取值范围为
,得m的取值范围为 或
或 .
.点评:解决的关键是根据直线与圆锥曲线的位置关系,联立方程组来结合韦达定理来得到,属于基础题。

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
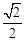 的椭圆
的椭圆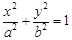 (a>b>0)的左、右焦点,直线
(a>b>0)的左、右焦点,直线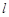 :x=-
:x=-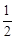 将线段F1F2分成两段,其长度之比为1 : 3.设A,B是C上的两个动点,线段AB的中点M在直线l上,线段AB的中垂线与C交于P,Q两点.
将线段F1F2分成两段,其长度之比为1 : 3.设A,B是C上的两个动点,线段AB的中点M在直线l上,线段AB的中垂线与C交于P,Q两点.
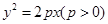 的焦点F的直线
的焦点F的直线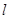 依次交抛物线及其准线于点A、B、C,若|BC |=2|BF|,且|AF|=3,则抛物线的方程是 。
依次交抛物线及其准线于点A、B、C,若|BC |=2|BF|,且|AF|=3,则抛物线的方程是 。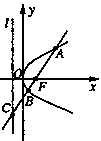
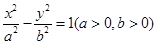 与抛物线
与抛物线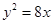 有一个公共的焦点
有一个公共的焦点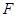 ,且两曲线的一个交点为
,且两曲线的一个交点为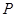 ,若
,若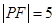 ,则双曲线的渐近线方程为.
,则双曲线的渐近线方程为.
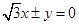
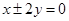
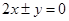
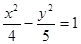 的离心率为首项,以函数
的离心率为首项,以函数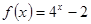 的零点为公比的等比数列的前
的零点为公比的等比数列的前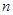 项的和
项的和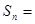
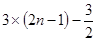
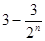
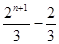
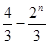
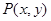 是抛物线
是抛物线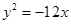 的准线与双曲线
的准线与双曲线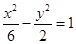 的两条渐近线所围成的三角形平面区域内(含边界)的任意一点,则
的两条渐近线所围成的三角形平面区域内(含边界)的任意一点,则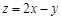 的最大值为_ __.
的最大值为_ __.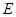 :
: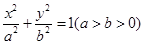 的左、右焦点分别为
的左、右焦点分别为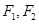 ,已知椭圆
,已知椭圆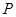 ,满足
,满足 ,过
,过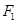 作垂直于椭圆长轴的弦长为3.
作垂直于椭圆长轴的弦长为3.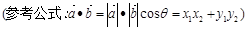
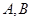 两点,求
两点,求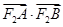 的取值范围.
的取值范围.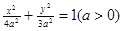 的左焦点为F,直线x=m与椭圆相交于点A、B,当△FAB的周长最大时,△FAB的面积是 .
的左焦点为F,直线x=m与椭圆相交于点A、B,当△FAB的周长最大时,△FAB的面积是 .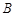 为双曲线
为双曲线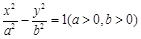 的左准线与x轴的交点,点
的左准线与x轴的交点,点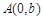 ,若满足
,若满足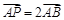 的点
的点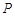 在双曲线上,则该双曲线的离心率为 .
在双曲线上,则该双曲线的离心率为 .